Деформирования порошковых материалов

Континуальные теории неупругого деформирования пористых и порошковых материалов строятся на результатах структурного моделирования. Макроскопические характеристики квазиоднородных несплошных тел получаются в результате осреднения локальных характеристик материала по принятому представительному объему, поэтому способ осреднения в итоге определяет адекватность континуальных моделей механического поведения пористых и порошковых тел.

При конструировании реологических моделей несплошных тел поровое пространство наделяют нулевыми материальными константами и мощность диссипируемой энергии связывают только с пластической или вязкой деформацией вещества. Статистическое осреднение локальных напряжений и скоростей деформаций проводят по всему объему твердой фазы [184]. Объем, по которому выполнено осреднение силовых или кинематических параметров, находится в однородном напряженно-деформированном состоянии (НДС), поэтому осреднение по всему объему вещества несплошного тела означает, что независимо от вида макроскопической деформации все вещество испытывает однородную деформацию растяжения-сжатия или сдвига [82, 184]. В рамках этой модели диссипативные функции несплошного тела D и его вещества с однородным НДС 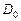будут связаны зависимостью

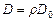, (3.37)

где r – объемная доля твердой фазы или относительная плотность. Из (3.37) следует эллиптическое условие пластичности для сжимаемых пористых тел с идеально-пластической твердой фазой [186, 230, 231]

, (3.38)

где s – среднее напряжение; Т – интенсивность касательных напряжений сдвига; t ₀ – предел текучести на сдвиг вещества твердой фазы; y, j – функции относительной плотности r. В (3.38) интенсивность касательных напряжений сдвига Т определяется через компоненты девиатора напряжений s_ij соотношением и отличается от используемой в [186, 230, 231] интенсивности касательных напряжений . Это приводит к появлению множителя 2 перед функцией y. При допущении об однородности полей деформаций или напряжений во всем объеме твердой фазы условие пластичности, аналогичное условию (3.38), получается как в рамках стохастических моделей [16, 46, 120, 169, 190], так и при обобщении гипотезы Бельтрами на пористые тела [34, 185].

Условие пластичности (3.38) часто применяют для порошков при схемах деформирования в замкнутых объемах с преобладанием сжимающих нагрузок [21, 31]. В разд. 1 отмечалось, что условие пластичности (3.38) не удовлетворяет граничным условиям по напряжениям для насыпной плотности порошка, когда r = r ₀. Так, в этом состоянии пластическая деформация порошка начинается при произвольно малых нагрузках, а из (3.38) следует, что для состояния насыпной плотности сопротивление порошка чистому сдвигу Т отлично от нуля: . Следовательно, структурная модель с осреднением локальных силовых и кинематических параметров по всему объему твердой фазы не может быть использована для порошкового тела.

Следуя работе [204], рассмотрим вариант структурной модели, учитывающий дискретно-контактную природу пластического деформирования порошковых тел.

Пусть порошковое тело нагружено однородным полем макронапряжений s_ij. Примем, что межчастичного скольжения нет, и уплотнение происходит за счет пластической деформации частиц. Выделим элементарную ячейку объемом V, в которую вписана деформированная частица порошка объемом V ₀. Мощность диссипации порошкового тела в ячейке при однородном поле макронапряжений будет равна

, (3.39)

где D – удельная мощность диссипации порошкового тела; 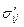, 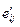– тензоры действительного неоднородного поля микроскопических напряжений и скоростей пластических деформаций в веществе ячейки. Вместо неоднородного поля напряжений 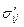и скоростей деформаций 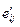введем эквивалентное ему однородное поле напряжений и скоростей деформаций . Пусть новое поле силовых и кинематических параметров занимает в веществе ячейки объем V _a, причем V _a £ V ₀. Условие эквивалентного перехода сформулируем в виде равенства мощности диссипации действительных неоднородных и эквивалентных им однородных полей напряжений и скоростей деформаций:

. (3.40)

Подынтегральное произведение в левой части (3.40) представляет собой диссипативную функцию пластического вещества 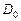с однородным НДС. С учетом (3.40) тождественное равенство диссипативных функций ячейки порошкового тела D и вещества ячейки 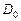запишется в виде

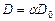, (3.41)

где 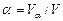- объемная доля вещества ячейки с однородными полями микроскопических напряжений и скоростей пластических деформаций.

Рассмотрим основное энергетическое уравнение для материального элемента объемом V _a и поверхностью S _a:

, (3.42)

где 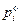– поверхностные напряжения; – скорости перемещения. Из (3.42) следует, что объем V _a будет ограничен контактными площадками, на которых 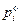¹ 0. Для уточнения формы контактных объемов сечением А, параллельным контактной площадке и удаленным от нее на расстояние z = h, выделим элемент частицы (рис. 3.3). Напряжения 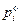на контактной площадке площадью S _к и нормалью n представим в виде суммы векторов нормальных 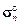и касательных 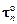напряжений, приложенных в центре тяжести площадки. Внутри сечения А находится область площадью S_{А a} с однородным НДС, которое характеризуется векторами нормальных и касательных 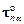напряжений. 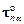Векторы и приложены в центре тяжести площадки S_{А a}. Для однородного НДС должны выполняться следующие условия:

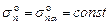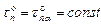; . (3.43)

Выясним, какой вид деформации частицы отвечает условиям однородности. С сечением А свяжем систему декартовых координат, направив ось z вдоль вектора 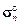, а ось у – параллельно вектору 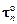. Из уравнения равновесия элемента

; (3.44)

следует, что касательные напряжения на контактной площадке 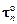вызывают изгиб и неоднородное распределение нормальных напряжений 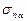по области S_{А a}. Кроме того, напряжения изгиба 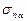возрастают пропорционально расстоянию h, поэтому при принятом допущении об однородном НДС контактные площадки должны быть свободны от касательных напряжений, и элемент частицы испытывает только центральное одноосное сжатие.

Для определения формы площадки S_{А a} свяжем с контактной площадкой S _к систему декартовых координат, направив ось z параллельно вектору . Начало координат поместим в произвольную точку границы контактной площадки (рис. 3.4). Положение центров тяжести площадок в принятой системе координат определяют радиус-векторы r_{c к} и r_{c a}. Векторы r _0к и r _0a, равные и противоположные векторам r_{c к} и r_{c a}, в системе координат, связанной с центром тяжести, характеризуют форму площадок, поэтому координаты центров тяжести, взятые с противоположным знаком, будут однозначно соответствовать координатам точек границ площадок. Координаты центра тяжести С _a(х _сa, у _сa, h) площадки S_{А a} и центра тяжести С _к(х _ск, у _ск, 0) площадки S _к определим из следующих уравнений равновесия:

; ;

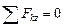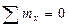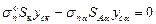; ; (3.45)

; .

Учитывая, что 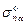= , получим, что центры тяжести площадок имеют одинаковые координаты х, у

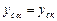, (3.46)

и находятся на общей нормали к площадкам. Аналогичным образом будут расположены любые две точки границ площадок S _к и S_{А a}, и эти площадки имеют одинаковую форму. Следовательно, вещество ячейки с однородным НДС будет находиться внутри прямого цилиндра с контактной площадкой в основании (рис. 3.5).

Р и с. 3.4. Схема деформирования частицы порошка нор - мальными напряжениями	Р и с. 3.5. Схема одноосного сжатия частицы порошка

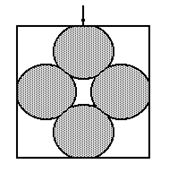
Таким образом, в связи с локальным нагружением частицы через контактную площадку единичный объем осреднения кинематических и силовых параметров представляет собой прямой цилиндр с контактной площадкой в основании. Суммарный объем осреднения V_a будет состоять из совокупности цилиндров, построенных на всех контактных площадках частицы и имеющих общее ядро, образованное пересечением образующих цилиндров. В целом пластически деформируемое порошковое тело представляет собой хаотично ориентированную контактно-стержневую систему, которая состоит из цилиндров, контактирующих своими основаниями, и испытывает однородную деформацию растяжения-сжатия (рис. 3.6).

a а	r б
Р и с. 3.6. Структурные модели деформируемого порошкового тела с осреднением по контактному (а) и полному (б) объемам вещества

При установлении количественной связи между диссипативными функциями порошкового тела D и вещества ячейки D_a не требуется выполнять прямое вычисление объема V_a. Для этого достаточно знать долю контактного объема a. Вероятностный анализ структурных характеристик порошковых материалов выполнен в [9, 55]. Согласно М.Ю. Бальшину [9] доля контактного объема a для текущей относительной плотности r составляет

. (3.47)

Зависимость a (r), полученная Г.Н. Ждановичем [55], имеет следующий вид:

. (3.48)

Здесь b – эмпирическая константа, которая для моносферических порошков равна b = 1. Уравнение, аналогичное уравнению (3.47) при b = 1, получено в [41] из модели уплотнения за счет роста радиусов сферических частиц вокруг фиксированных центров с дальнейшим перекрытием сфер и образованием шеек контакта. В состоянии насыпной плотности (r = r ₀) объемная доля пластически деформируемого вещества a = 0 и, согласно (3.41), диссипативная функция D порошкового тела также равна нулю. Тем самым обеспечивается выполнение граничных условий по сопротивлению деформации для начального насыпного состояния порошка.

В работе [157] показано, что уравнения (3.47) и (3.48) являются вариантами решения одного и того же дифференциального уравнения, составленного на основе общих представлений о статистическом характере контактного взаимодействия частиц. Уравнение (3.47) получено при условии, что в процессе уплотнения возможно не только образование, но и разрыв контактов частиц. Зависимость (3.48) следует из предположения, что при деформации происходит лишь увеличение каждого единичного контактного сечения частиц при их сближении. Расчетные значения a, полученные по формулам (3.47) и (3.48), близки и различаются не более чем на 10% (рис. 3.7). Однако преимущество уравнения М.Ю. Бальшина (3.47) состоит в том, что при определении эмпирической константы b оно легко линеаризуется.

Р и с. 3.7. Зависимость объемной доли контактного объема от относительной плотности: 1 – уравнение М.Ю. Бальшина; 2 – уравнение Г.Н. Ждановича

Для решения краевых задач пластического деформирования порошковых тел необходимо знать определяющие соотношения между макроскопическими напряжениями и скоростями деформации . Зависимость следует из определения диссипативной функции:

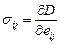. (3.49)

С учетом (3.41) уравнение (3.49) запишется следующим образом:

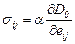. (3.50)

Чтобы воспользоваться соотношением (3.50), необходимо установить функциональную зависимость между диссипативной функцией вещества 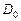и макроскопическими скоростями деформации порошкового тела с различной реологией твердой фазы. Диссипативная функция 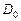выражается через интенсивность скоростей деформации сдвига несжимаемого вещества w и его реологические константы [188, 232]:

линейно-вязкое тело

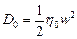; (3.51, а)

идеально-пластическое тело

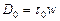; (3.51, б)

нелинейно-вязкое тело

. (3.51, в)

Диссипативная функция нелинейно-вязкого тела (3.51, в) следует из степенного закона сопротивления вязкому течению .

В итоге задача сводится к определению зависимости интенсивности микроскопической скорости деформации сдвига w от макроскопических скоростей деформации . Для определения искомой связи w () воспользуемся теорией вязкого и пластического течения пористых тел, изложенной в работах [186, 188, 232]. В основу теории положена следующая гипотеза: зависимость осредненной интенсивности скоростей деформации сдвига твердой фазы w от макроскопических скоростей деформаций инвариантна относительно реологических свойств твердой фазы. На основании этой гипотезы находится зависимость w () для линейно-вязкого тела, а затем выполняется обобщение на тела другой реологии.

Для линейно-вязкого сжимаемого материала диссипативная функция имеет вид

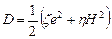, (3.52)

где е – макроскопическая скорость объемной деформации; Н – интенсивность макроскопических скоростей деформации сдвига; z, h – коэффициенты объемной и сдвиговой вязкости. Коэффициенты вязкости z и h пористого тела выражаются через коэффициент сдвиговой вязкости вещества h ₀ и функции пористости. В разд. 1 уже указывалось, что в настоящей работе используются функции y и j, полученные В.В. Скороходом методом самосогласования [184]. В этом случае коэффициенты вязкости z и h связаны с функциями пористости зависимостями [186, 230]

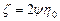; (3.53)

и функции y и j имеют вид

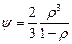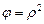; . (3.54)

После подстановки в соотношение (3.41) зависимостей (3.51, а), (3.52) и (3.53) найдем выражение w () для линейно-вязкого порошкового тела:

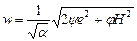. (3.55)

Определяющие уравнения порошковых тел с различной реологией твердой фазы получим из (3.50) с учетом зависимостей (3.51) и (3.55):

линейно-вязкое тело

; (3.56)

идеально-пластическое тело

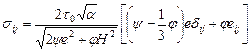; (3.57)

нелинейно-вязкое тело

. (3.58)

Из определяющих соотношений (3.57) несложно получить условие пластичности порошкового тела с идеально-пластической твердой фазой:

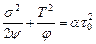. (3.59)

Уравнение (3.59) описывает только процесс уплотнения порошка по механизму пластического сдвига частиц.

Следует отметить, что в определяющие уравнения для линейно-вязкого порошкового тела не входит параметр a, который характеризует количество вещества, диссипирующего механическую энергию. Определяющие уравнения (3.56) идентичны уравнениям, полученным в [184, 188] при осреднении по всему объему твердой фазы, количественной мерой которого служит относительная плотность r. Таким образом, линейно-вязкое сжимаемое тело оказалось инвариантно к способу осреднения локальных напряжений и скоростей деформаций по объему вещества. Этот результат следует связать с квадратичной формой диссипативной функции линейно-вязкого тела. Для идеально-пластического и нелинейно-вязкого порошков, находящихся в состоянии насыпной плотности, когда a = 0, деформирующие напряжения равны нулю. Так как для порошкового тела диссипация имеет место при a > 0, то уравнение (3.56) можно применять только при плотности, большей, чем насыпная плотность.

В качестве экспериментальной проверки предложенной структурной модели пластически деформируемого порошкового тела рассмотрим процесс изостатического прессования металлических порошков. На рис. 3.8 приведены опытные данные по уплотнению при изостатическом прессовании сферических порошков свинца и олова, взятые из работы [100]. На этом же рисунке представлены зависимости между относительной плотностью r порошка и относительным давлением p /2t₀, рассчитанные по условиям пластичности (3.38), (3.59) и уравнению изостатического прессования, предложенному в [200]:

. (3.60)

Для расчета объемной доли пластически деформируемого вещества a в (3.59) использовалась зависимость (3.47). Относительная насыпная плотность r ₀ принималась r ₀ = 0, 5 (получено экстраполяцией опытных данных для олова) и значение показателя степени
b = 1. Из рис. 3.8 видно, что наилучшее соответствие расчетных и экспериментальных данных во всем диапазоне изменения плотности показывает контактно-стержневая модель и связанное с ней условие пластичности (3.59). Расхождение расчетных и экспериментальных данных для порошка свинца следует связать с более низкой, чем
r ₀ = 0, 5, насыпной плотностью этого материала.

r/2t0

Р и с. 3.8. Зависимость относительного давления изостатического прессования от относительной плотности порошков: 1 – расчет по (3.38); 2 – расчет по (3.60); 3 – расчет по (3.59); эксперимент: · – олово; o – свинец

Величина давления при уплотнении порошкового тела пропорциональна объемной доле пластически деформируемого вещества. Структурные модели, из которых следуют уравнения (3.38) и (3.60), не учитывают локализацию пластического течения при контактном взаимодействии частиц и предполагают пластическое деформирование всего объема вещества, поэтому расчет по уравнениям (3.38) и (3.60) показывает более высокие значения относительного давления по сравнению с экспериментом. Соответственно осреднение микроскопических параметров по всему объему твердой фазы дает верхнюю оценку, а осреднение в пределах контактных объемов частиц – нижнюю оценку макроскопических свойств порошкового материала.