Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Характеристики уравнений прессования
|
|
| Константы уравнения прессования | Материал оболочки | ||
| Песок | Шамотная крошка | Песок + шамотная крошка | |
| r 0 А n m | 0, 61 0, 96 1, 75 | 0, 41 1, 85 1, 75 | 0, 56 1, 1 1, 75 |
Феноменологические параметры условия пластичности (3.64) находили в два этапа. Сначала определяли показатель степени b формулы (3.65) и эффективный предел прочности tb. Для этого уравнения (3.64) записывали следующим образом:
; (3.85, а)
. (3.85, б)
Здесь через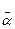 
обозначено выражение 
в уравнении М.Ю. Бальшина (3.65) для относительной доли контактного объема a. В координатах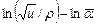 
уравнению (3.85, б) будет соответствовать прямая линия. По параметрам линейного участка зависимости (3.85) находили значения показателя b и эффективную характеристику прочности твердой фазы t 0. Затем по известным значениям показателя b и доли контактного объема a определяли характеристики внутреннего трения f, K 0 и давление р *. Для этого уравнения (3.64) приводили к виду
; 
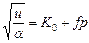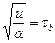(3.86)
и исследовали их зависимость от гидростатического давления р. Если априори положить b = 1, что допустимо для сферических порошков, то процедура нахождения реологических характеристик упрощается и ограничивается анализом зависимостей (3.86).
На рис. 3.11 приведены результаты обработки экспериментальных данных по прессованию песка в закрытой матрице. В координатах 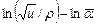зависимости (3.85) представляют собой две прямые линии. Уравнение (3.85, б) описывает деформирование порошка в области больших значений плотности и давлений, и ему соответствует верхняя прямая на рис. 3.11, а. При аппроксимации этой прямой определены значения показателя b = 1, 06 и эффективного предела прочности частиц песка tb = 160 МПа. Затем из графических зависимостей (3.86), представленных на рис. 3.11, б, получены оценки коэффициента внутреннего трения f = 1, 97, константы сцепления K 0 = 85 МПа и давления p * = 38 МПа. Сводные данные по феноменологическим параметрам условия пластичности (3.64) для исследованных материалов приведены в табл. 3.2.
Точка излома на графиках рис. 3.11 отражает изменение механизма пластического течения – прекращается межчастичное скольжение и начинается разрушение частиц песка. Из решения уравнения (3.67) F = 0 определено значение плотности rF = 0, 724, начиная с которого уплотнение может происходить только за счет дробления частиц песка. Отметим, что это значение rF незначительно отличается от относительной плотности плотнейшей упаковки монодисперсных сфер, составляющей r = 0, 74 [3].
Т а б л и ц а 3.2
|
|