Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Примеры решения задач. Задача1.В однородном магнитном поле с индукцией В = 0,1 Тл равномерно вращается рамка, содержащая N = 100 витков

Задача1. В однородном магнитном поле с индукцией В = 0, 1 Тл равномерно вращается рамка, содержащая N = 100 витков, с частотой п = 10 с^-1. Площадь S рамки равна 150 см². Определить мгновенное значение э.д.с. 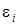, соответствующее углу поворота рамки в 30º.

Дано: Решение.

В = 0, 1 Тл Физическую систему в данной задаче составляет магнитное поле

N = 100 витков и помещённая в него рамка.

п = 10 с^-1 Мгновенное значение э.д.с. индукции 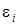определяется основным

S = 150 см² уравнением электромагнитной индукции Фарадея – Максвелла:

= 30º

. (7.9)

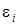-? Потокосцепление 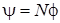, где N – число витков, пронизываемых

магнитным током 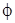. Подставив выражение в формулу (7.9),

получим

(7.10)

При вращении рамки магнитный поток 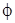, пронизывающий рамку в момент времени t, изменяется по закону 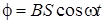, где В – магнитная индукция; S – площадь рамки; ω – круговая частота. Подставив в формулу (7.10) выражение 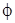и продифференцировав по времени, найдём мгновенное значение э.д.с. индукции:

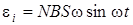. (7.11)

Круговая частота ω связана с частотой п вращения соотношением . Подставив выражение в формулу (7.11) получим

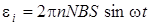. (7.12)

Произведя вычисления по формуле (7.12), найдём

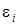= 47, 1 В.

Ответ: 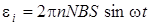= 47, 1 В.

Задача 2. Обмотка соленоида состоит из одного слоя плотно прилегающих друг к другу витков медного провода диаметром d = 0, 2 мм. Диаметр D соленоида равен 5 см. По соленоиду течёт ток силой I = 1 А. Определить заряд Q, протекающий через обмотку, если концы её замкнуть накоротко. Толщиной изоляции пренебречь.

Дано: Решение.

d = 0, 2 мм Физическую систему в данном случае составляет соленоид и соз-

D = 5 см даваемое им магнитное поле.

I = 1 А Возможны два способа решения. 1-й способ. Заряд dQ, который
протекает по проводнику за время dt при силе тока I, определяется

Q -? равенством

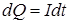. (7.13)

Полный заряд, протекающий через проводник за время t, будет . Сила тока в данном случае убывает экспоненциально со временем и выражается формулой (7.8):

.

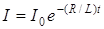Внося выражение силы тока I под знак интеграла, и интегрируя от 0 до ∞
(при t → ∞ I → 0), получим

.

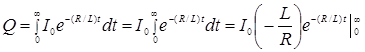Подставим пределы интегрирования и определим количество электричества, протекающее через обмотку:

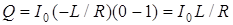. (7.14)

Далее по аналогии с первым способом.

2-й способ. Подставив в формулу (7.13) вместо силы тока I выражение её через э.д.с. индукции 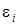и сопротивление R соленоида, т.е. , найдём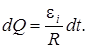

Но 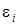связана со скоростью изменения потокосцепления ψ по закону Фарадея – Максвелла: , тогда

.

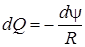Интегрируя, получаем

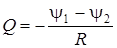. (7.15)

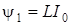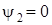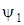Потокосцепление ψ пропорционально силе тока в соленоиде. Следовательно, , , так как соответствует тому моменту, когда ток в цепи обратится в нуль. Подставив выражение и в формулу (7.15), получим , или

что совпадает с формулой (7.14).

Для определения заряда, протекающего через обмотку соленоида, следует найти индуктивность L соленоида и сопротивление R обмотки соленоида, которые выражаются формулами:

где μ ₀ – магнитная постоянная; N – число витков; l ₁ – длина соленоида; 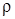- удельное сопротивление провода; l – длина провода; S – площадь сечения провода; d – диаметр провода; d ₁ – диаметр соленоида.

Подставив найденные выражения L и R в формулу (7.14), получим

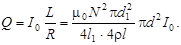(7.16)

Заметим, что длина провода l может быть выражена через диаметр d ₁ соленоида соотношением 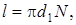где N – число витков, тогда формуле (7.16) можно придать вид:

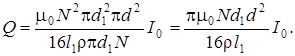
Но есть диаметр провода, так как витки плотно прилегают друг к другу. Следовательно,

(7.17)

Произведя вычисления по формуле (7.17), получим

Q = 363 мкКл.

Ответ: = 363 мкКл.

Задача 3. Плоская рамка в виде равностороннего треугольника со стороной а = 10^-1 м находится в магнитном поле, индукция которого изменяется по закону = (α + β t ²) ,

где α = 10^-1 Тл, β = 10^-2 Тл/с², – единичный вектор оси Ох. Плоскость рамки составляет угол φ = 30º с направлением индукции магнитного поля (рис.7.1).Определить количество теплоты, которое выделяется в рамке за первые
2 с, если сопротивление рамки R = 0, 01 Ом. Индуктивностью и ёмкостью контура пренебречь.

Дано: Решение.

= (α + β t ²) Физическую систему в данном случае составляет изменяю-
α = 10^-1 Тл щееся во времени магнитное поле, а, следовательно, и из-

β = 10^-2 Тл/с² меняющийся магнитный поток; проводящая рамка, распо-

φ = 30º ложенная в этом поле; возникшее вихревое электрическое

R = 0, 01 Ом поле и созданный этим полем индукционный ток. Коли-

t = 2 с чество теплоты, которое выделяется в рамке, можно найти

а = 10^-1 по формуле:

Q -? 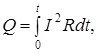(7.18)

где I – индукционный ток, возникающий в рамке, который согласно закону Ома,

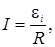(7.19)

где 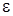_i – э.д.с. индукции.

Для нахождения э.д.с. индукции воспользуемся законом Фарадея:

.

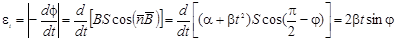Рис.7.1.

Учитывая, что площадь рамки 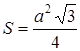, sin 30º = 1/2, получаем

(7.20)

Выражение (7.19) с учётом (7.20) можно записать

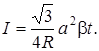(7.21)

Подставляя (7.21) в выражение (7.18), получаем:

Дж.

Ответ: 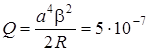Дж.

Задача 4. По соленоиду течёт ток силой I = 2 А. Магнитный поток 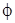, пронизывающий поперечное сечение соленоида, равен 4 мкВб. Определить индуктивность L соленоида, если он имеет N = 800 витков.

Дано: Решение.

I = 2 А Физическую систему в данном случае составляет соленоид

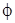= 4 мкВб и создаваемое им магнитное поле.

N = 800 витков Индуктивность L соленоида связана с потокосцеплением ψ

соотношением , откуда 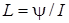. Заменив здесь пото-

L -? косцепление ψ его выражением через магнитный поток 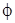и

число витков N соленоида (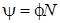), получим:

(7.22)

После вычисления по формуле (7.22) найдём:

L = 1, 6 мГн.

Ответ: 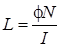= 1, 6 мГн.

Задача 5. При скорости изменения силы тока Δ I /Δ t в соленоиде, равной 50 А/с, на его концах возникает э.д.с. самоиндукции ε _i = 0, 08 В. Определить индуктивность L соленоида.

Дано: Решение.

Δ I /Δ t = 50 А/с Физическую систему в данном случае составляет соленоид и

ε _i = 0, 08 В создаваемое им магнитное поле.

Индуктивность соленоида связана с э.д.с. самоиндукции и ско-

L -? ростью изменения силы тока в его обмотке соотношением

т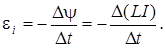

Вынося постоянную величину L за знак приращения, получим:

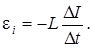(7.23)

Опустив знак «минус» в этом равенстве (направление э.д.с. в данном случае несущественно) и выразив интересующую нас величину – индуктивность, получим:

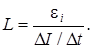(7.24)

Сделав вычисления по этой формуле, найдём: L = 1, 6 мГн.

Ответ: 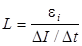= 1, 6 мГн