Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

II. 12. Сила Лоренца.

Сила, действующая со стороны магнитного поля на электрический заряд Q, движущийся в этом поле со скоростью , называется силой Лоренца и выражается формулой

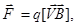(2.11)

где 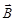– индукция магнитного поля, в котором заряд движется.

Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор 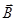, а четыре вытянутых пальца направить вдоль вектора скорости положительного заряда, то отогнутый под углом 90⁰ большой палец покажет направление силы, действующей на положительный заряд. На рис. 2.16 показана взаимная ориентация векторов 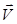, 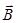и для положительного заряда. На отрицательный заряд сила действует в противоположном направлении. Модуль силы Лоренца равен

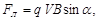
где α – угол между и .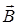

Рис. 2.16

II. 13. Движение заряженных частиц в магнитном поле под действием силы Лоренца?

а) Если заряженная частица массой m влетает параллельно силовым линиям, то на нее магнитное поле не действует, сила Лоренца F_л=0. Траектория ее движения есть прямая линия (рис. 2.17).

Рис. 2.17

б) Если заряженная частица движется в магнитном поле со скоростью , перпендикулярной вектору , то сила Лоренца (рис. 2.18) постоянна по модулю и нормальна к траектории частицы. Согласно 2-му закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определяется из условия qVB = mV²/r, откуда

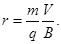
Рис. 2.18

Период вращения частицы, т. е. время Т, за которое она совершит один полный оборот,

Или с учетом r

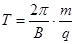
в) Если скорость заряженной частицы направлена под углом α к вектору (рис. 2.19), то ее движение можно представить в виде суперпозиции:

1) равномерного прямолинейного движения вдоль поля со скоростью

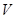= соs α;

2) равномерного движения со скоростью 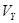= 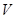sin α по окружности в плоскости, перпендикулярной полю. Радиус окружности определяется формулой

В результате сложения обоих движений возникает движение по спирали, ось которого параллельна магнитному полю.

Рис. 2.19

Шаг винтовой линии

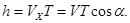
Подставив сюда Т, получим выражение,

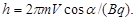
Направление, в котором закручивается спираль, зависит от знака заряда частицы.

Если скорость заряженной частицы составляет угол α с направлением вектора 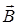неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то r и h уменьшаются с ростом 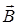. На этом основана фокусировка заряженных частиц в магнитном поле.