Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Уравнения плоской, сферической волн.

В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид

ξ 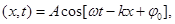(3.3)

где А = const – амплитуда волны, ω – циклическая частота, φ ₀ – начальная фаза волны, определяемая в общем случае выбором начала отсчета х и t, [ 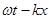+ φ ₀ ] – фаза плоской волны.

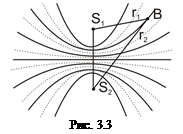
Уравнение сферической волны ( волны, волновые поверхности которой имеют вид концентрических сфер), записывается как

ξ (r, t)= 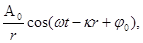(3.3)

где r – расстояние от центра волны до рассматриваемой точки среды. В случае сферической волны даже в среде, не поглощающей энергию, амплитуда колебаний не остается постоянной, а убывает с расстоянием по закону 1/r. Уравнение (3.3) справедливо лишь для r, значительно превышающих размеры источника (тогда источник колебаний можно считать точечным).

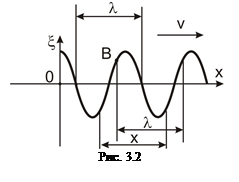4. Длина упругой волны, распространяющейся вдоль оси Х.

Расстояние между ближайшими частицами, колеблющихся в одинаковой фазе, называется длиной волны λ (рис. 3.2)

Длина волны равна тому расстоянию, на которое распространяется определенная фаза колебаний за период, т.е.

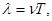
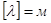(3.2)

или, учитывая, что Т = 1/ν, где ν – частота колебаний,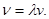

волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называетсяволновым фронтом.