
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения задач. Задача 1.В схеме (рис. 4.1) внутреннее сопротивление источника с э.д.с
|
|
Задача 1. В схеме (рис. 4.1) внутреннее сопротивление источника с э.д.с. 1 В равно 0, 1 Ом. Сопротивления R 1, R 2 и R 3 соответственно равны 5 Ом, 4 Ом и 3 Ом. Найти токи, текущие через сопротивления R 1 и R 2.
| Дано: ε = 1 В r = 0, 1 Ом R 1 = 5 Ом R 2 = 4 Ом R 3 = 3 Ом |  Рис. 4.1
Рис. 4.1
|
| I 1 -? I 2 -? |
Решение.
Рассмотрим, каким образом соединены сопротивления в данной цепи и заменим эти соединения на эквивалентные сопротивления. Сопротивления R 2 и R 3 соединены последовательно, их можно заменить эквивалентным сопротивлением
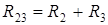 (см. (4.9)). (4.11)
(см. (4.9)). (4.11)
Тогда исходная цепь примет вид, показанный на рис. 4.2.
Так как R 2 и R 3 соединены последовательно, сила тока на сопротивлениях R 2, R 3 и R 23 будет одинакова и равна I 2.
Сопротивления R 1 и R 23 на рис. 4.2 соединены параллельно. Заменим их эквивалентным сопротивлением R 123 (см. (4.10.)):
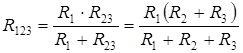 (4.12)
(4.12)
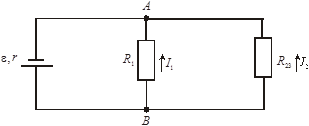
Рис. 4.2
Сила тока через это сопротивление:
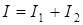 . (4.13)
. (4.13)
Запишем закон Ома для замкнутой цепи (рис.4.2) после замены сопротивлений R 1 и R 23 на эквивалентное R 123:
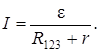 (4.14)
(4.14)
Рассмотрим напряжение на сопротивлениях R1 и R23. Из закона Ома для однородного участка (4.3) следует:
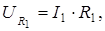 (4.15)
(4.15)
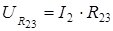 . (4.16)
. (4.16)
А так как эти участки соединены параллельно,
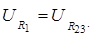 (4.17)
(4.17)
С учётом (4.13) – (4.17) составим систему уравнений:

Выразим 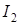 из (4.20), подставим в (4.18) и приравняем с (4.19):
из (4.20), подставим в (4.18) и приравняем с (4.19):
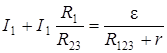 . (4.21)
. (4.21)
Отсюда 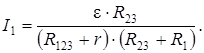
С учётом (4.11) и (4.12):
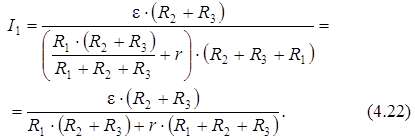
Силу тока через резистор R 2 найдём из (4.20):
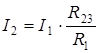 или с учётом (4.11):
или с учётом (4.11):
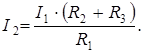
Подставим числовые значения:
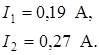
Ответ: 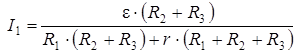 = 0, 19 (А),
= 0, 19 (А),
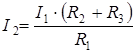 = 0, 27 (А).
= 0, 27 (А).
Задача 2. Потенциометр с сопротивлением R = 100 Ом, э.д.с. ε которого равна 150 В и внутреннее сопротивление r = 50 Ом (рис. 4.3). Определить показание вольтметра с сопротивлением RВ = 500 Ом, соединенного одной из клемм потенциометра подвижным контактом, установленным посередине потенциометра. Какова разность потенциалов между теми же точками потенциометра при отключенном вольтметре?
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
| Дано: R = 100 Ом ε = 150 В r = 50 Ом RВ = 500 Ом | 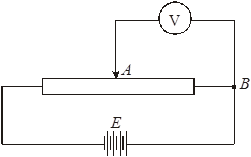 Рис. 4.3
Рис. 4.3
|
| U 1, U 2 -? |
Решение.
Показание U 1 вольтметра, подключенного к точкам А и В (рис.4.3), определяются по формуле:
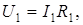 (4.23)
(4.23)
где I 1 – cила тока в неразветвлённой части цепи; R 1 – сопротивление параллельно соединённых вольтметра и половины потенциометра.
Силу тока I1 найдём по закону Ома для всей цепи:
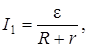 (4.24)
(4.24)
где R – сопротивление внешней цепи.
Внешнее сопротивление R есть сумма двух сопротивлений:
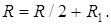 (4.25)
(4.25)
Сопротивление R 1 параллельного соединения может быть найдено по формуле 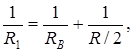 откуда
откуда

Подставив в эту формулу числовые значения величин и произведя вычисления, найдём
 Ом.
Ом.
Подставив в выражение (4.24) правую часть равенства (4.25), определим силу тока:
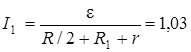 А.
А.
Если подставить значение I 1 в R 1 в формулу (4.23), то найдём показания вольтметра:
U 1 = 46, 9 В.
Разность потенциалов между точками А и В при отключённом вольтметре равна произведению силы тока I 2 на половину сопротивления потенциометра, т.е.  , или
, или
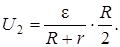
Подставив сюда значения величин ε, R и r, получим
U 2 = 50 В.
Ответ: 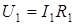 = 46, 9 В;
= 46, 9 В; 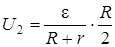 = 50 В.
= 50 В.
Задача 3. Сила тока в проводнике сопротивлением R=12 Ом равномерно убывает от I0=5A до I=0 в течении времени t=10c. Какое количество теплоты Q выделяется в этом проводнике за указанный промежуток времени.
| Дано: R=12 Ом I0=5A I1=0 t1=10cек | Решение:
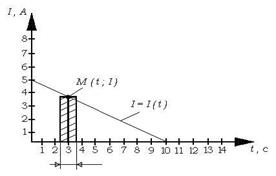
1.Выполним чертеж графика изменения силы тока со временем:
|
| Q(дис)-? | |
2. Составим уравнение прямой изменения силы тока от времени:
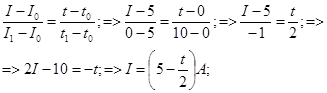
3. Выделим произвольную точку 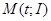 на прямой I=I(t), запишем элементарное количество тепла, выделяющегося в проводнике сопротивлением R за время
на прямой I=I(t), запишем элементарное количество тепла, выделяющегося в проводнике сопротивлением R за время 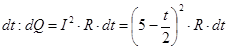
4. Найдем искомое количество тепла выделившегося на сопротивлении за время 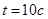 :
:
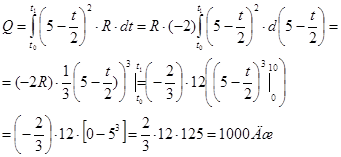
Ответ: 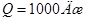
Задача 4. Источники тока с э.д.с. ε 1 = 10 В и ε 2 = 4 В включены в цепь, как показано на рис. 4.4. Определить силы токов, текущих в сопротивлениях R 2 и R 3, если R 1 = 2 Ом,
R 2 = R 3 = 4 Ом. Внутреннее сопротивление источников тока r 1 = 0, 5 Ом, r 2 = 0, 2 Ом.
| Дано: ε 1 = 10 В ε 2 = 4 В R 1 = 2 Ом R 2 = R 3 = 4 Ом r 1 = 0, 5 Ом r 2 = 0, 2 Ом | 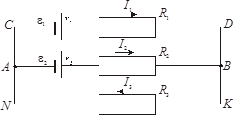 Рис. 4.4
Рис. 4.4
|
| I 2 -? I 3 -? |
Решение.
Цепь, изображённая на рис. 4.4, является разветвлённой, т.к. имеет два узла (т. А и т. В). Для расчёта сил токов в таких цепях используют правила Кирхгофа. Направления токов на участках с сопротивлениями R1, R2 и R3 покажем на рис. 4.4 произвольно. Запишем первое правило Кирхгофа (4.7.) для узла А:
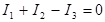 . (4.26)
. (4.26)
Чтобы записать второе правило Кирхгофа, выберем направление обхода контуров ABKN – по часовой стрелке. В уравнении (4.26) три неизвестных. Составим ещё два уравнения по второму правилу Кирхгофа и решим систему. Если направление тока совпадает с направлением обхода, произведение IR берётся со знаком «+», в противном случае – со знаком «-». Значение э.д.с. считается положительным, если при обходе контура внутри источника осуществляется переход от минуса к плюсу. В противном случае э.д.с. входит в уравнение со знаком «-». С учетом вышесказанного и (4.8) для контуров ACDB и ABKN соответственно получим:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
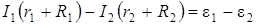 ; (4.27)
; (4.27)
 (4.28)
(4.28)
Подставим в уравнения (4.27) и (4.28) числовые значения и запишем систему:
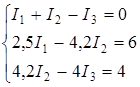
Найдём силы токов методом определителей (детерминантов). Для этого перепишем систему в виде:
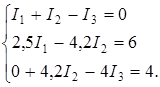
Искомые значения сил токов будут равны:
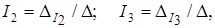 (4.29)
(4.29)
где Δ – определитель системы уравнений; 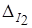 и
и 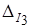 – определители, полученные заменой соответствующих столбцов определителя Δ столбцами, составленными из свободных членов трёх вышеприведённых уравнений. Находим:
– определители, полученные заменой соответствующих столбцов определителя Δ столбцами, составленными из свободных членов трёх вышеприведённых уравнений. Находим:
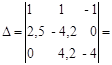 -37, 3
-37, 3
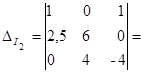 14
14
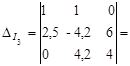 -52
-52
Отсюда получим I 2 ≈ -0, 375 А; I 3 ≈ 1, 39 А.
Ответ: I 2 ≈ -0, 375 А (знак «-» означает, что действительное направление тока противоположно направлению, показанному в условии); I 3 ≈ 1, 39 А.
Задача 5. К амперметру с сопротивлением 300 Ом присоединён шунт, понижающий чувствительность амперметра в 10 раз. Какое сопротивление надо подключить в цепь последовательно, чтобы присоединение шунта не изменило сопротивление исходной цепи?
| Дано: RА = 300 Ом Im ´ = nIm n = 10 | Решение.
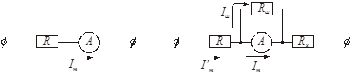 а) б)
Рис. 4.5
а) б)
Рис. 4.5
|
| Rx -? |
На рис. 4.5 изображена цепь до (а) и после (б) присоединения шунта. До присоединения шунта максимальное отклонение стрелки амперметра вызвал ток в цепи силой Im, после присоединения - в п раз больший 
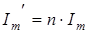 . При этом непосредственно через амперметр сила тока не изменилась (см. рис. 4.5, б). Следовательно:
. При этом непосредственно через амперметр сила тока не изменилась (см. рис. 4.5, б). Следовательно:
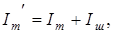
где Iш – сила тока через шунт.
Отсюда:
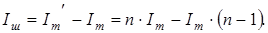 (4.30)
(4.30)
Так как шунт присоединяется к амперметру параллельно, то их общее сопротивление согласно (4.10):
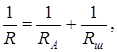
где Rш – сопротивление шунта, RА – сопротивление амперметра. Отсюда:
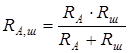 . (4.31)
. (4.31)
Сопротивление Rх присоединено к участку с сопротивлением RА, ш последовательно, поэтому согласно требованиям условия задачи и в соответствии с
рис. 4.5, а и 4.5 б:
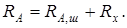
Отсюда, с учётом (4.31):
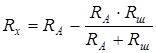 . (4.32)
. (4.32)
Так как шунт и амперметр соединены параллельно, то напряжения на них равны:
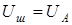 (4.33)
(4.33)
или с учётом закона Ома (4.3)
 .
.
Выразим отсюда Rш с учётом (4.30):
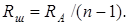
Подставим (4.33) в (4.32):
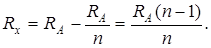
Подставим числовые значения:
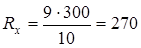 Ом.
Ом.
Ответ: 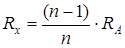 = 270 Ом.
= 270 Ом.
Задача 6. Электрическая цепь содержит N одинаковых аккумуляторов, каждый из которых имеет внутреннее сопротивление r. Внешняя цепь потребляет одинаковую мощность, как при последовательном, так и при параллельном соединении аккумуляторов. Найдите сопротивление внешней цепи.
| Дано: N r | Решение.
Мощность, потребляемая во внешней цепи, равна:
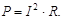 Для того, чтобы найти сопротивление внешней цепи, используем условие равенства мощностей, а, следовательно, и сил токов при параллельном и последовательном включении аккумуляторов.
Для того, чтобы найти сопротивление внешней цепи, используем условие равенства мощностей, а, следовательно, и сил токов при параллельном и последовательном включении аккумуляторов.
|
| R -? |
Если аккумуляторы соединены последовательно, то их общее сопротивление согласно (4.9):
 (4.34)
(4.34)
В этом случае по закону Ома для замкнутой цепи (4.4):
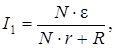 (4.35)
(4.35)
где 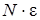 - суммарная э.д.с. батареи аккумуляторов, ε – э.д.с. одного аккумулятора.
- суммарная э.д.с. батареи аккумуляторов, ε – э.д.с. одного аккумулятора.
При параллельном включении э.д.с. батареи будет равна ε, а суммарное сопротивление аккумуляторов (4.10):
 (4.36)
(4.36)
Тогда закон Ома (4.4) будет иметь вид:
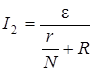 . (4.37)
. (4.37)
Приравниваем I 1 и I 2: 
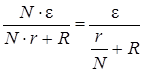 . (4.38)
. (4.38)
Отсюда получим: R = r.
Ответ: R = r.
|
|
