
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Упражнения. 1) Если А – линейный оператор евклидова пространства V, то f(x, y) = (Ax, y), g(x, y) = (x, Ay) – билинейные формы
|
|
1) Если А – линейный оператор евклидова пространства V, то f(x, y) = (Ax, y), g(x, y) = (x, Ay) – билинейные формы. Докажите это.
2) Докажите, что билинейная форма f(x, y) = (Ax, y) симметрична тогда и только тогда, когда А – самосопряженный линейный оператор.
3) Пусть e 1, e 2, …, en и 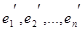 – базисы линейного пространства V, С – матрица перехода от первого базиса ко второму, А и
– базисы линейного пространства V, С – матрица перехода от первого базиса ко второму, А и 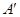 – матрицы билинейной формы в этих базисах. Докажите, что
– матрицы билинейной формы в этих базисах. Докажите, что 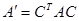 .
.
4) Найдите матрицу билинейной формы и запишите соответствующую ей квадратичную форму а) 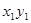 (
( ; б)
; б) 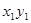 (
(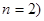 ; в)
; в) 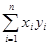 ; г)
; г) 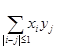 .
.
5) Приведите с помощью невырожденного линейного преобразования переменных к каноническому виду (для которого матрица диагональная) билинейную форму:
а) 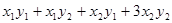 ; б)
; б) 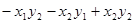 ;
;
в) 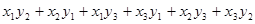 .
.
6) Покажите, что функция
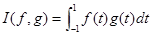
является симметричной билинейной формой в пространстве многочленов степени 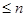 . Приведите ее к каноническому виду при n = 3.
. Приведите ее к каноническому виду при n = 3.
7) Докажите, что ранг билинейной функции равен 1 тогда и только тогда, когда она является произведением двух ненулевых линейных функций.
8) Функция f(x, y) называется инвариантной относительно линейного оператора  линейного пространства V, если
линейного пространства V, если 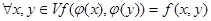 . Докажите, что все невырожденные линейные операторы, относительно которых функция f(x, y) инвариантна, образуют мультипликативную группу.
. Докажите, что все невырожденные линейные операторы, относительно которых функция f(x, y) инвариантна, образуют мультипликативную группу.
9) Найдите все линейные операторы двумерного линейного пространства, относительно которых инвариантна билинейная форма 
|
|
