Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Применение квадратичных форм к исследованию линий и поверхностей второго порядка

Общим уравнением второй степени называется уравнение

F (x ₁, …, x_n) = 0, (1)

где F (x ₁, …, x_n) – многочлен второй степени от n переменных x ₁, …, x_n. Многочлен F (x ₁, …, x_n) можно представить в виде суммы квадратичной формы f, линейной формы (однородного многочлена первой степени) и свободного члена с. Если через А обозначить матрицу квадратичной формы f, через Х – столбец неизвестных x ₁, …, x_n и через В – столбец из коэффициентов b ₁, b ₂, …, b_n линейной формы, то в матричном виде многочлен F можно записать в виде

F (x ₁, …, x_n) = Х ^Т АХ + 2Х ^Т В + с. (2)

При n = 2 уравнение (1) задает уравнение линии второго порядка на плоскости R ², а при n = 3 – уравнение поверхности второго порядка в пространстве R ³.

В аналитической геометрии для общего уравнения линии на плоскости или поверхности в пространстве ставится задача отыскания новой декартовой прямоугольной системы координат, в которой уравнение данной линии или поверхности принимает наиболее простой вид. Переход от одной декартовой прямоугольной системы координат к другой может быть осуществлен в два приема:

1) параллельный перенос начала координат в новую точку с сохранением направления осей;

2) поворот осей при сохранении начала.

Формулы параллельного переноса начала, выражающие старые координаты точки через ее новые координаты, имеют вид

x_i = v_i + y_i, 1 ,

где v_i – координаты нового начала относительно старой системы координат(n = 2 или 3). Если через Х мы обозначим столбец из старых координат x_i, через Y – столбец новых координат y_i и через V – столбец из старых координат нового начала, то формулы параллельного переноса можно записать в виде матричного равенства

X = V + Y. (3)

Формулы поворота осей вокруг неподвижного начала в матричной форме могут быть записаны так

X = QY, (4)

где Q – ортогональная матрица второго или третьего порядка.

Решим задачу упрощения уравнения при произвольном n. Уточним предъявляемые требования:

1) избавиться от слагаемых, содержащих произведения разных переменных;

2) если возможно, то избавиться от слагаемых первой степени;

3) если возможно, то избавиться от свободного члена.

Уравнение, полученное при соблюдении этих требований, называется каноническим.

Задача. При помощи преобразования X = QY с ортогональной матрицей Q в многочлене Х ^Т АХ + 2Х ^Т В + с нельзя избавиться от слагаемых, содержащих переменные в первой степени. Докажите это.

Решение. 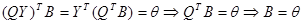. Если в многочлене

Х ^Т АХ + 2Х ^Т В + с есть слагаемые первой степени, т.е. В 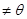, то и в преобразованном многочлене они есть.

Задача. Всегда ли возможно при помощи преобразования X = V + Y в многочлене Х ^Т АХ + 2Х ^Т В + с избавиться от слагаемых, содержащих переменные в первой степени?

Решение. Подвергнем многочлен преобразованию

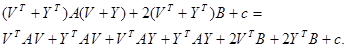
Как матрица квадратичной формы матрица А симметрична. Матрица 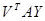первого порядка и поэтому совпадает со своей транспонированной:

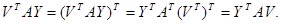
Введем обозначение 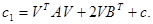В преобразованном многочлене

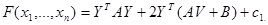
первые степени отсутствуют, если столбец V удовлетворяет условию 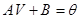. А это матричное уравнение относительно неизвестного столбца V не всегда разрешимо. При произвольном столбце В разрешимость можно гарантировать лишь при невырожденной матрице А. Если матричное уравнение разрешимо, то при помощи преобразования 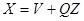с ортогональной матрицей Q многочлен F приводится к каноническому виду. Этот случай соответствует в аналитической геометрии центральным линиям и поверхностям второго порядка.

Предположим, что уравнение 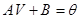не разрешимо относительно столбца V. Это может случиться только при невырожденной матрице А. Подвергнем переменные многочлена (2) ортогональному преобразованию, при котором квадратичная форма 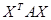примет канонический вид. Так как ранг r матрицы А меньше ее порядка, то число r квадратов переменных с отличными от нуля коэффициентами в каноническом виде меньше n и в результате преобразования многочлен примет вид:

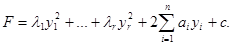
где 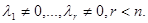Можно избавиться от первых степеней переменных 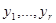при помощи параллельного переноса

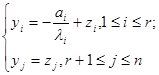
Многочлен примет вид

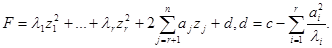
После преобразования

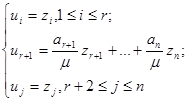
получим где . После выполнения параллельного переноса

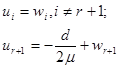
получим канонический вид

.

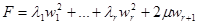Этот случай соответствует нецентральным линиям и поверхностям второго порядка.

Задача. Привести к каноническому виду уравнение линии:
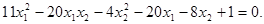