
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Приведение квадратичной формы к главным осям
|
|
Теорема. (о приведении квадратичной формы к главным осям). Любую квадратичную форму с помощью ортогонального преобразования переменных можно привести к каноническому виду.
Доказательство. Матрица А квадратичной формы симметрична, а для симметричной матрицы найдется ортогональная матрица Q такая, что матрица Q- 1 AQ диагональна. Подвергнув квадратичную форму ортогональному преобразованию с матрицей Q, мы приведем ее к каноническому виду. ■
Теорема. Квадратичная форма с помощью ортогонального преобразования переменных приводится к каноническому виду, коэффициентами которого являются корни характеристического многочлена матрицы квадратичной формы, взятые с их кратностями.
Доказательство. Пусть квадратичная форма f некоторым ортогональным преобразованием переменных приведена к каноническому виду
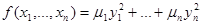
Легко видеть, что ортогональное преобразование оставляет инвариантной сумму квадратов переменных, поэтому

Квадрат определителя ортогональной матрицы равен 1. А определитель матрицы преобразованной квадратичной формы отличается от определителя матрицы исходной квадратичной формы на квадрат определителя матрицы линейного преобразования. Отсюда,
 . ■
. ■
Следствие. Для любой ортогональной матрицы, приводящей к диагональному виду симметрическую матрицу, на главной диагонали полученной диагональной матрицы располагаются характеристические корни симметрической матрицы, взятые с их кратностями.
Пример. Приведите к главным осям квадратичную форму
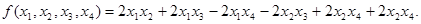
Матрица квадратичной формы имеет вид
А = 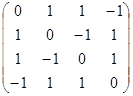 .
.
Найдем ее характеристический многочлен
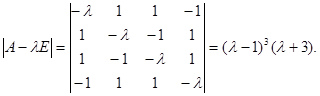
Матрица А имеет трехкратный характеристический корень 1 и простой характеристический корень – 3. Таким образом,
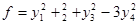 –
–
канонический вид, к которому квадратичная форма приводится ортогональным преобразованием.
Для нахождения ортогонального преобразования, осуществляющего это приведение, необходимо найти собственные векторы линейного оператора, матрицей которого в некотором ортонормированном базисе является матрица А. При  для этого надо решить однородную систему линейных уравнений
для этого надо решить однородную систему линейных уравнений
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение

Ранг системы равен 1 и поэтому фундаментальная система решений состоит из трех решений. Например,
b 1 = (1, 1, 0, 0),
b 2 = (1, 0, 1, 0),
b 3 = (-1, 0, 0, 1).
Ортогонализируя эту систему, получим
с 1 = b 1 = (1, 1, 0, 0),
с 2 =  с 1 + b 2 = (
с 1 + b 2 = ( ,
,  , 1, 0),
, 1, 0),
с 3 =  с 1 +
с 1 + 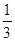 с 3 + b 3 = (
с 3 + b 3 = ( ,
, 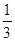 ,
, 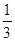 , 1).
, 1).
При  надо решить однородную систему линейных уравнений
надо решить однородную систему линейных уравнений

Ранг системы равен 3 и поэтому фундаментальная система решений состоит из одного решения. Например, с 4 = (1, -1, -1, 1).
Нормируя ортогональную систему векторов с 1, с 2, с 3, с 4, получим ортонормированную систему векторов

Таким образом, форма приводится к главным осям ортогональным преобразованием:
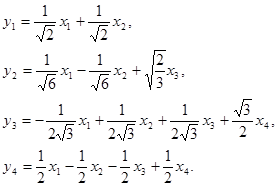
Следует отметить, что ответ неоднозначен.
|
|
