Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Учет симметрии при раскрытии статической неопределимости

Определим, прежде всего, для статически неопределимых систем следующие виды симметрии:

a) Симметричная система с симметричной нагрузкой:

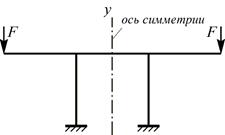
Здесь и сама система и приложенная к ней нагрузка зеркально симметричны относительно оси симметрии у.

b) Симметричная система с кососимметричной нагрузкой:

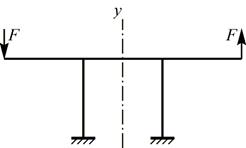
Здесь, в отличие от предыдущего случая, при зеркальной симметрии относительно оси у, направление приложенных сил получается противоположное.

c) Кососимметричная система с симметричной нагру зкой:

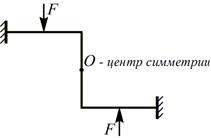
Здесь, при повороте одной половины системы относительно центра симметрии О на 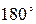, она полностью совпадает со второй своей половиной. Направление сил при этом тоже совпадает.

d) Кососимметричная система с кососимметричной нагрузкой:

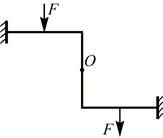
Здесь, в отличие от предыдущего случая, при повороте на 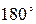половинки системы совпадают, но направление сил получается противоположное.

Для статически неопределимых систем, обладающих одним из перечисленных видов симметрии, процесс раскрытия статической неопределимости существенно упрощается, если рассматривать саму систему как внутренне статически неопределимую. Для этого необходимо образовать основную систему путем разрезания исходной системы по оси или по центру симметрии на две статически определимых системы.

Проследим применение алгоритма метода сил на примере симметричной системы с симметричной нагрузкой.

Исходная система:

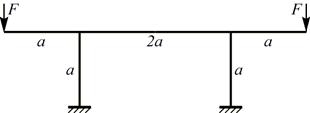
Основная система:

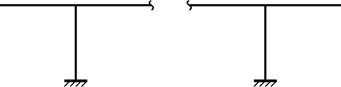
Эквивалентная система:

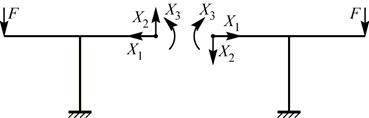
При таком выборе основной системы в качестве «лишних» неизвестных выступают внутренние силовые факторы в проведенном сечении, причем, продольная сила Х₁ и изгибающий момент Х₃ – симметричные ВСФ, а поперечная сила Х₂ – кососимметричный внутренний силовой фактор.

Построим вспомогательные эпюры: грузовую и единичные.

Грузовая эпюра М_F:

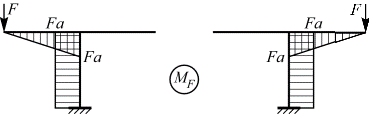симметричная эпюра

Единичные эпюры M₁, М₂ и М₃:

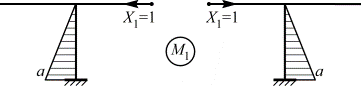симметричная эпюра

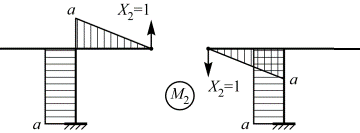кососимметричная эпюра

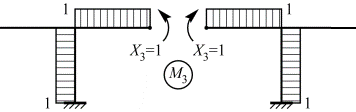симметричная эпюра

Эпюры M₁, М₃ и М_F, построенные от действия симметричных силовых факторов являются симметричными эпюрами, а эпюра М₂, построенная от действия кососимметричного силового фактора, является кососимметричной эпюрой.

Очевидно, что коэффициенты СКУМС, полученные путем «перемножения» симметричной эпюры на кососимметричную, равны нулю, т.е. 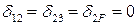. Тогда система канонических уравнений метода сил примет следующий вид:

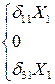
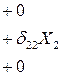
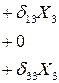
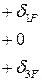
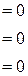
Эта система трех уравнений с тремя неизвестными распадается на две более простые подсистемы, решить которые существенно проще:

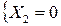
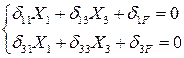
Таким образом, учет симметрии понижает степень статической неопределимости.