Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Запись условия эквивалентности.

Условием эквивалентности двух систем (эквивалентной статически определимой и исходной статически неопределимой) является отсутствие перемещений раскрепленных точек эквивалентной системы по направлению отброшенных связей (т.е. в направлении действия «лишних» неизвестных).

В строке №4 Таблицы 2 записаны условия эквивалентности для рассматриваемых примеров.

Для n раз статически неопределимой системы условие эквивалентности выглядит следующим образом:

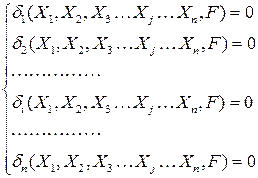
На основании принципа суперпозиции данную систему можно записать в виде:

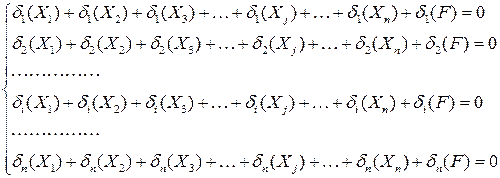
Таблица 2

№ п/п	Алгоритм метода сил	Растяжение-сжатие	Кручение	Изгиб
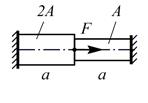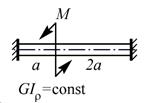1.	Расчетная схема	s=1	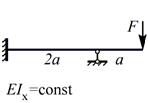s=1	s=1
2.	Выбор основной системы (возможные варианты)	№1: №2:	№1: №2:	№1: №2:
3.	Образование эквивалентной системы (для варианта №1 основной системы)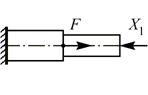
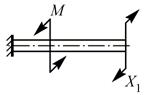
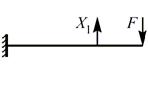
4.	Условие эквивалентности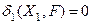
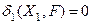
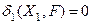
5.	СКУМС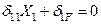
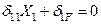
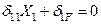
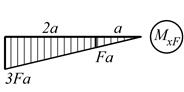
6.	Построение грузовой эпюры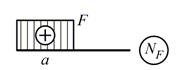
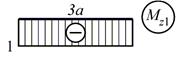
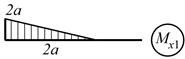
7.	Построение единичной эпюры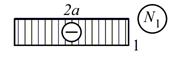
8.	Вычисление единичного коэффициента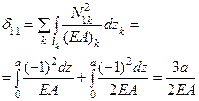
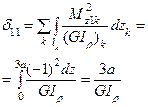
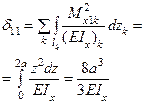
9.	Вычисление грузового коэффициента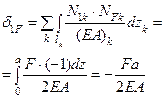
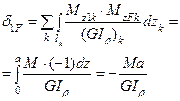
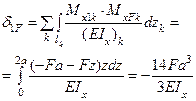
10.	Решение СКУМС (определение неизвестной Х1)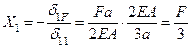
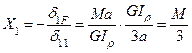
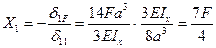
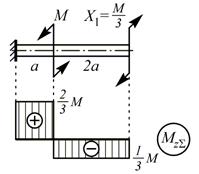
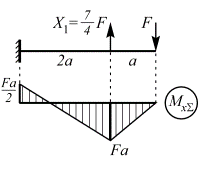
11.	Построение суммарной эпюры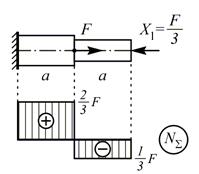
12.	Деформационная проверка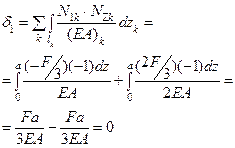

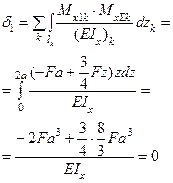
Чтобы выделить в условии эквивалентности неизвестные Х проведем следующие рассуждения на примере 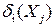– перемещения i-той точки под действием силы Х_j. На основании закона Гукаможно сделать заключение, что величина 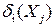будет во столько раз отличаться от перемещения 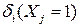под действием единичной силы, находящейся на месте силы Х_j, во сколько раз сила Х_j отличается от единицы, т.е. в Х_j раз.

Таким образом: . Для простоты обозначим 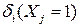как 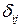. То есть первый индекс будет обозначать номер (положение) раскрепленной точки или убранной связи (i), а второй – положение единичной силы, совпадающее с положением другой убранной связи (j). С учетом такого обозначения систему уравнений можно записать в каноническом виде:

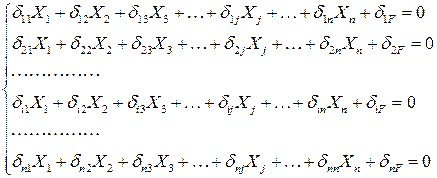(3.1)

Итак, (1.1) – система канонических уравнений метода сил (СКУМС). Коэффициенты 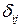при неизвестных X_j называются единичными коэффициентами, а свободные члены – 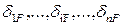– грузовыми слагаемыми. Физическая сущность всех коэффициентов – это перемещение соответствующих точек упругой системы, обозначенных первым индексом от фактора либо единичного, либо грузового, обозначенного вторым индексом.

Условия эквивалентности в каноническом виде для рассматриваемых примеров – см. строку №5 Таблицы 2.