Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свободные колебания упругой системы с одной степенью свободы
|
|
Пусть тележка массой m, прикрепленная к стенке пружиной жесткостью c, выводится из состояния равновесия кратковременным возмущением, действующим вдоль оси z.
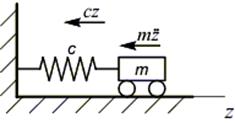
На рассматриваемую систему действуют сила упругости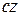 
и сила инерции 
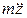(здесь 
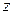– величина смещения тележки от положения равновесия, 
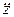– ускорение). В соответствии с принципом Даламбера запишем сумму проекций сил на ось z:
,
.
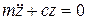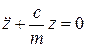Обозначим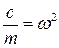 
.
Таким образом, дифференциальное уравнение, описывающее свободные колебания упругой системы с одной степенью свободы без учета сил сопротивления имеет вид:
.
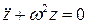Решение данного дифференциального уравнения можно представить в виде:
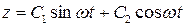
или
,
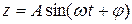где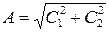 
– амплитуда, w – собственная частота колебаний упругой системы, j – начальная фаза.
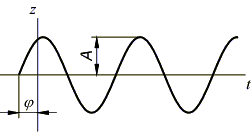
Таким образом, свободные (собственные) колебания представляют собой простые гармонические колебания.
Запишем жесткость пружины в виде
,
где d 11 – податливость упругой системы.
Тогда частота собственных колебаний
.
|
|
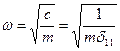