Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Оценка значимости коэффициента корреляции и коэффициентов уравнений регрессии.

Оценка значимости коэффициента корреляции

Поскольку коэффициент корреляции r определяется по данным случайной выборки, то он может отличаться от коэффициента корреляции r, который соответствует генеральной совокупности.

В случае, когда объем выборки N ³ 20, то предполагают, что коэффициент корреляции является случайной величиной, распределенной по нормальному закону.

Пусть s_r – среднеквадратичное отклонение выборочного коэффициента корреляции r. Тогда при N ³ 20 доверительный интервал для r будет равен (r - x_ps_r, r + x_ps_r), где х_р– параметр нормального распределения вероятностей:

.

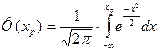Значение х_р определяется по таблице функции распределения Ф(х) в зависимости от вероятности Р. Для оперативного определения значения х_р при Р ³ 0, 9, можно использовать таблицу 2.

Таблица 2.

Значение среднеквадратичного отклонения s_r можно определить по формуле .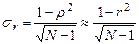

Подставим в доверительный интервал вместо неизвестной величины r его оценку по выборке r и s_r. Тогда

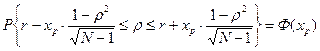. Для проверки значимости выборочного коэффициента корреляции r чаще используется так называемая нулевая гипотеза: H₀: r = 0 (H₁: r ¹ 0).

Суть нулевой гипотезы состоит в том, что в случае, когда для случайных величин х и y на основании выборок 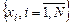и 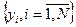получено½ r½ > 0, т.е. между ними имеется корреляционная связь, предполагается, что в генеральной совокупности этой связи нет (H₀: r = 0).

При r = 0, получим:

.

При проверке нулевой гипотезы достаточно использовать только левый (нижний) предел доверительного интервала 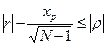. Так как r = 0, то .

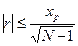Данное условие означает, что нулевая гипотеза с вероятностью Ф(х_р) подтверждается.

Если 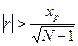, то нулевая гипотеза с вероятностью Ф(х_р) отвергается, а, следовательно, связь между х и y имеет место.

В тех случаях, когда размер выборки N< 30, для проверки нулевой гипотезы (r = 0) используется t – критерий Стьюдента.

Алгоритм использования t – критерия Стьюдента

1. а) Для анализа значимости коэффициента корреляции 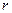определяется расчетное значение 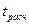по формуле 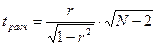(если N< 30)

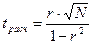(если N> 30)

б) Для анализа значимости частного коэффициента корреляции 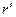определяется расчетное значение t_{расч .} по формул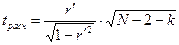е: , где 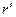- частный коэффициент корреляции, k – номер частного коэффициента корреляции (k – число исключенных факторов).

в) Для анализа значимости корреляционного отношения 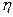определяется расчетное значение t_{расч .} по формуле:

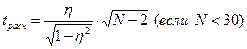
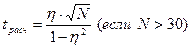
2. По таблице критических точек распределения Стьюдента по значению числа степеней свободы k = N - n (n – число параметров) и уровню значимости a (уровень значимости - это вероятность совершить ошибку первого рода, т.е. отвергнуть правильную нулевую гипотезу) определяется теоретическое значение t_теор. (критическая точка).

Таблица 3.

Таблица критических точек для a=5%

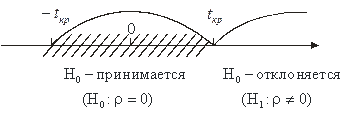
Рис.1.

Если ½ t_расч½ £ t_теор., то нулевая гипотеза Н₀ принимается (r = 0), если ½ t_расч½ > t_теор., то Н₀ – отвергается (r ¹ 0), следовательно, случайные величины х и y коррелированы, то есть между ними существует линейная связь, следовательно:

a) коэффициент корреляции r значим;

b) частный коэффициент корреляции 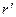значим;

c) корреляционное отношение 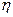значимо.

Оценка значимости коэффициентов уравнений регрессии

В общем случае значимость коэффициентов уравнений регрессии определяется с помощью t – критерия Стьюдента.