
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Регрессионный анализ. Регрессионный анализ – раздел математической статистики, главная задача которого состоит в выводе на основании соответствующих выборочных совокупностей
|
|
Регрессионный анализ – раздел математической статистики, главная задача которого состоит в выводе на основании соответствующих выборочных совокупностей уравнения регрессии, устанавливающего связь между значениями зависимой (эндогенной) переменной (результирующим показателем) и значениями независимых (экзогенных) переменных.
Указанную связь будем записывать в виде: 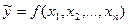 , где
, где 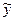 - результирующий показатель;
- результирующий показатель; 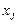 – j-й независимый параметр (фактор, воздействующий на результирующий показатель (
– j-й независимый параметр (фактор, воздействующий на результирующий показатель ( )).
)).
Совокупность методов, определяющих тесноту связи между y и xj, составляет другой раздел математической статистики - корреляционный анализ. Если связь между переменными y и x является нефункциональной, установлена на основании совместного анализа соответствующих им выборок y 1, y2, …, yN и x1, x2, …, xN, то считается, что между ними существует корреляционная связь.
Регрессия называется парной, если на y действует только один фактор (n = 1), и множественной, если число факторов, воздействующих на y, более одного (n > 1).
Уравнение линии регрессии (линии связи) при парной регрессии записывается в виде: ỹ = f (x).
Если при функциональной зависимости y=f(x) одному значению независимой переменной х соответствует только одно значение зависимой переменной y, то при корреляционной зависимости каждому значению х может соответствовать сколь угодно много значений y. Поэтому изменение х при корреляционной зависимости вызовет изменение не конкретного y, а среднего значения 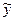 , и это изменение будет тем больше, чем теснее y и х будут корреляционно зависимы.
, и это изменение будет тем больше, чем теснее y и х будут корреляционно зависимы.
Тесноту связи определяют с помощью коэффициента корреляции r, который находится в пределах 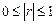 .
.
Если r = 0, то между случайными величинами y и х линейной связи нет (может иметь место параболическая, степенная, логарифмическая и т.п. связь, но не линейная 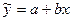 ).
).
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Если 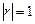 , то между величинами y и х существует функциональная связь: y = f (x).
, то между величинами y и х существует функциональная связь: y = f (x).
При r > 0 имеет место прямая зависимость, т.е. с увеличением х увеличивается y, а при r < 0 – обратная зависимость - с увеличением х уменьшается y.
Если 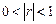 , то между случайными величинами y и х существует только корреляционная связь:
, то между случайными величинами y и х существует только корреляционная связь: 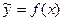 .
.
Коэффициент корреляции находится по формуле:
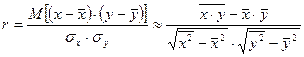 , (1)
, (1)
 где
где
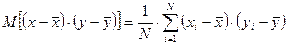
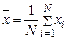 ,
,  ,
, 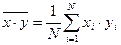 ,
, 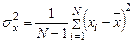
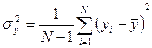
Для вычисления r по значениям выборочных данных xi и yi, 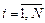 , формулу (1) преобразуем к виду (2):
, формулу (1) преобразуем к виду (2):
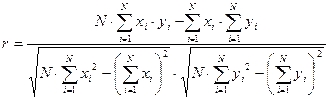 (2)
(2)
|
|
