Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Множественная линейная регрессия
|
|
Множественная линейная регрессия является простейшим формой множественной зависимости. Ее уравнение записывается в виде 
(1)
где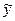 
- результирующий показатель (зависимая переменная); 
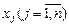- независимый фактор.
Запишем уравнения (1) в матричной форме.
Пусть Х – матрица N наблюдений по n факторам (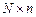
),
Y - матрица – столбец наблюдений по результирующему показателю (1 х N),
A - матрица-столбец неизвестных параметров уравнения регрессии (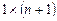
):
,
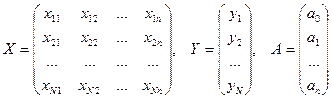где xij – i –ое (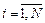
) наблюдение по j –ому (
) фактору.
Ввиду того, что размерность матрицы-столбца А есть 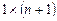, матрицу Х дополним слева столбцом из единиц и обозначим 
:
.
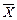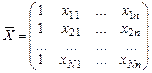Тогда уравнение (1) можно записать в матричном виде: 
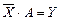(2). Транспонируем матрицу 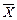(строки и столбцы поменяем местами, 
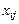превращаем в 
): 
, 
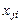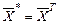где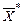 
- матрица, транспонированная к матрице .
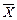Умножим левую и правую части уравнения (2) слева на матрицу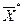 
: 
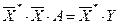(3).
Уравнение (3) является системой нормальных уравнений, полученной на основании уравнения регрессии (1) и записанной в матричной форме.
Пусть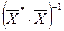 
– матрица, обратная матрице 
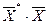. Тогда, умножив слева на эту матрицу левую и правую части уравнения (3), получим 
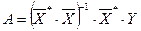. Откуда следует, что коэффициенты уравнения регрессии (1) могут быть определены по формуле:
,
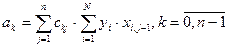где 
– элементы обратной матрицы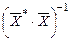 
.
Для уравнения с двумя объясняющими переменными (n=2)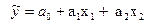 
: 
|
|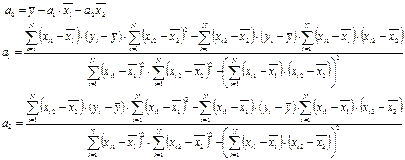