Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные виды уравнений парной регрессии и методы определения их параметров
|
|
Выбор формулы связи (вида уравнения) называется спецификацией уравнения регрессии.
Перечислим основные виды уравнений парной регрессии:
§ Линейная зависимость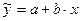 
;
§ Гиперболическая зависимость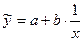 
;
§ Степенная зависимость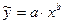 
;
§ Логарифмическая зависимость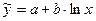 
;
§ Полиномиальная зависимость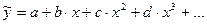 
;
§ Тригонометрическая зависимость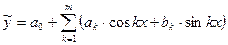 
; где m – число гармоник; a0, ak, bk – неизвестные коэффициенты линии регрессии.
Определение параметров уравнения регрессии называется параметризацией.
Для определения неизвестных параметров уравнения регрессии обычно применяют метод наименьших квадратов (МНК). Рассмотрим функцию вида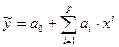 
.
Алгоритм применения МНК
1. Строится целевая функция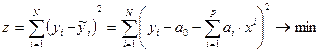 
2. Находится система уравнений для определения неизвестных параметров
Согласно МНК для нахождения параметров полинома p -ой степени необходимо решить систему так называемых нормальных уравнений:
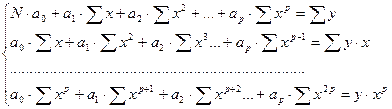
Решение этой системы относительно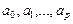 
и дает искомые значения параметров.
Линейная зависимость
Для определения неизвестных параметров линейной зависимости методом наименьших квадратов необходимо решить следующую систему нормальных уравнений:
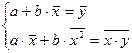. (3)
Пусть d, da, db – определители, соответствующие системе уравнений (3), а именно:
.
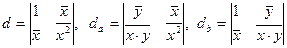Тогда неизвестные коэффициенты уравнения регрессии 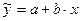будут равны:
.
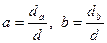Другое решение системы (3). Из первого уравнения следует: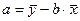 
, а из второго – имеем:
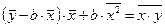
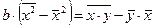
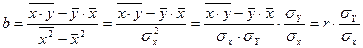Таким образом 
, 
.
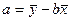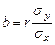Подставив значения а и b в формулу 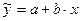, получим:
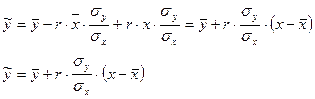
Гиперболическая зависимость
При гиперболической зависимости 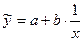параметры a и b находят, как и в случае линейной зависимости, но для уравнения регрессии 
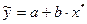, где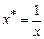 
.
Степенная зависимость
Для определения параметров a и b степенной зависимости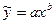 
необходимо преобразовать зависимость в линейную, для этого необходимо прологарифмировать обе части:
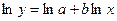
Пусть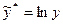 
, a* = lna, x* = lnx, тогда 
.
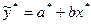Применив к зависимости МНК, находим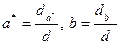 
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Определители d, da*, db относятся к системе уравнений
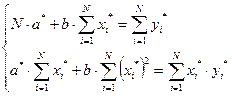, где
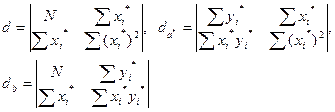
Значение а находим в результате потенцирования a = ea*, значение b из соотношения b = db / d.
Логарифмическая зависимость
Для определения параметров a и b при заданной зависимости 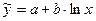уравнение регрессии представим в виде 
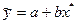, где x*=lnx..
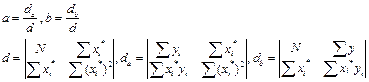
Параболическая зависимость
Алгоритм применения МНК для параболической зависимости второго порядка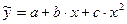 
заключается в следующем:
- Строится целевая функция:
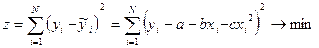
- Находится система нормальных уравнений
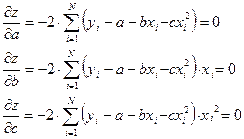
Система преобразуется к виду:
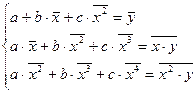
Решение системы нормальных уравнений относительно неизвестных параметров a, b, c можно найти, как и при линейной зависимости, с помощью определителей:
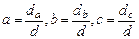, где
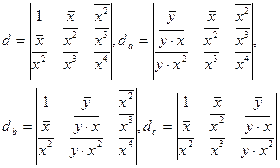
Алгоритм применения МНК для параболической зависимости третьего порядка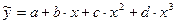 
заключается в следующем:
- Строится целевая функция:
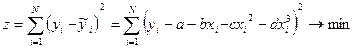
- Находится система нормальных уравнений
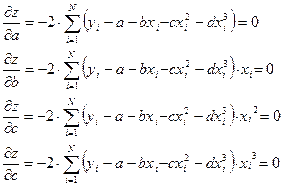
Система преобразуется к виду:
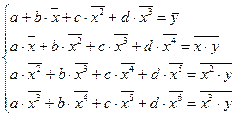
Решение системы нормальных уравнений относительно неизвестных параметров a, b, c, d можно найти, как и при линейной зависимости, с помощью определителей:
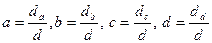, где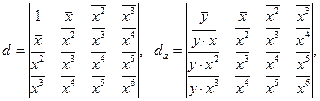 
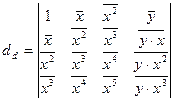
Тригонометрическая зависимость
Уравнение регрессии этого вида является приближением функции y (х), которое тем точнее, чем больше значение m (m - число гармоник, количество составляющих исследуемого процесса). Поэтому при различных значениях m получаются различные виды тригонометрической зависимости.
Значения неизвестных параметров a0, ak, bk (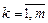
) находят с помощью метода наименьших квадратов.
Для этого строится целевая функция:
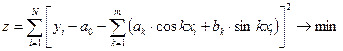Далее находят 
.
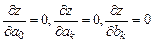Получается система нормальных уравнений. Эта система обладает свойством ортогональности.
В результате решения системы получим:
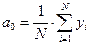
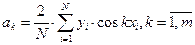
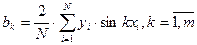
Если в качестве фактора xi рассматривается фактор времени (например, при построении тригонометрического тренда), то xi заменяем на величину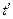 
, где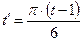 
, для помесячных данных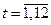 
Таблица 1.
месяцы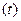 
| ||||||||||||
уровни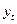 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
|
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
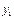
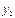
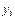
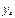
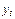
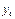
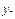
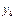
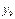
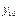
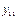
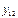
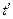
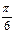
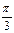
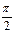
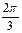
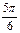
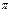
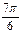
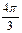
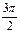
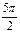
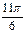
Например, при k=1 тригонометрический тренд имеет вид: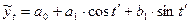 
, где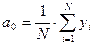 
, 
, 
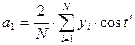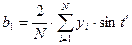
Если объем выборки N больше 12 месяцев, то 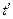для первых 12-ти месяцев изменяется от 0 до 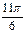, затем в следующем году 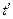снова изменяется от 0 до 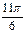, и так повторяется для каждого последующего года.
Если увеличивается число коэффициентов в уравнении регрессии при параболической и тригонометрической зависимости, то увеличится точность аппроксимации, но уменьшится значимость в результате увеличения дисперсии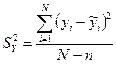 
, где n – количество неизвестных параметров в уравнении регрессии.
При нелинейной зависимости определение тесноты связи между двумя случайными величинами х и y производится с помощью корреляционного отношения
, 
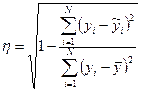где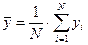 
.
|
|