Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Точность методов Монте-Карло. Пусть в задаче приближенного вычисления неизвестной величины по методу Монте-Карло со случайной величиной ( и вектором независимых случайных величин
|
|
Пусть в задаче приближенного вычисления неизвестной величины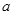 
по методу Монте-Карло со случайной величиной 
(
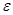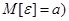и вектором независимых случайных величин 
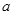ставится дополнительное условие о том, что вычисленное значение должно отличаться от на малую величину 
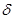с вероятностью не меньше заданной 
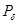(близкой к 1). Каким образом следует выбирать число 
суммируемых величин для удовлетворения дополнительного условия?
Формально дополнительное условие имеет вид:
.
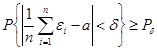Для оценки количества требуется вычислить вероятность в левой части неравенства, и для вычисления в некоторых случаях допустимо использовать независимость величин 
и асимптотическую нормальность суммы:
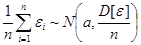при 
,
где
,
.
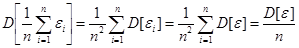Таким образом,
,
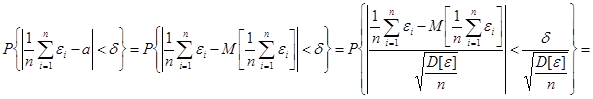
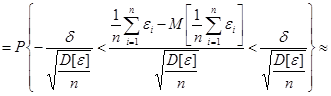
Откуда,
,
,
,
 .
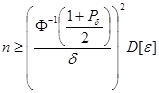| (10.4) |
Если дисперсия 
может быть вычислена аналитически, тогда из (10.4) можно определить число . Если же дисперсию не удается вычислить аналитически, то допустимо использовать верхнюю оценку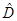 
, 
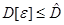, вместо дисперсии в (10.4). В некоторых случаях в (10.4) вместо дисперсии используют выборочную дисперсию:
,
где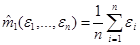 
.
Из соотношения (10.4) следует:
а) количество требуемых испытаний прямо пропорционально дисперсии , поэтому следует стараться выбрать величину 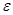таким образом, чтобы дисперсия оказалась как можно меньше (при условии, что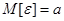 
).
б) при увеличении точности в 10 раз (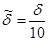
) требуемое количество слагаемых возрастает в 100 раз.
|
|