Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Метод получения случайной величины с заданной функцией распределения.

Пусть – случайная величина, имеющая равномерное распределение (или распределение «близкое» к ), полученная одним из методов, представленных выше.

Если требуется получить случайную величину непрерывного типа с функцией распределения , имеющей обратную функцию , тогда образуем случайную величину :

.

Легко видеть, что функция распределения есть функция действительно:

,

, , – функция распределения величины .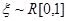

Если требуется получить случайную величину дискретного типа, принимающую конечное число значений , , …, с вероятностями , , 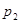…, , тогда образуем случайную величину :

.

Легко видеть, что случайная величина принимает значение 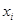с вероятностью :

,

.

Строго говоря, получить случайную величину дискретного типа, принимающую счетное число значений , , … с вероятностями , 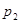…, не представляется возможным. Тем не менее, поскольку ряд составленный из вероятностей сходится, то остаток ряда стремиться к нулю, отсюда следует, что можно выбрать число такое, что , где 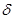малое число (например, ). 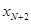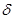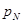Случайная величина принимает значения , , … с малой вероятностью (меньше чем ), поэтому этими значениями на практике можно пренебречь и приписать оставшуюся вероятность к вероятности значения . В этом случае, воспользовавшись методом, представленным выше, можно получить случайную величину, принимающую конечное число значений , …, , с вероятностями , …, , .

Если требуется получить случайную величину смешанного типа, то необходимо комбинировать представленные выше методы: если для полученного значения определена обратная функция , то следует положить , если же для полученного значения обратная функция не определена (в силу разрыва в некоторой точке 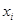величины ), то следует положить .

42. Применение метода Монте-Карло в задаче приближенного вычисления числа и в задаче приближенного вычисления характеристик сложной случайной величины. Точность методов Монте-Карло. 