Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Определение 9.5.

Коэффициентом детерминации называется число:

.

В координатной форме коэффициент детерминации имеет вид:

.

Коэффициент детерминации отражает меру расхождения между наблюдением и регрессионными значениями , отнесенную к вариации наблюдения .

Определение 9.6.

Скорректированным коэффициентом детерминации называется величина:

.

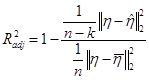По-прежнему из двух вариантов регрессии лучшей следует считать ту, для которой величина больше.

Постановка задачи нормальной линейной регрессии, связь между оценкой по методу наименьших квадратов и оценкой максимального правдоподобия. Теорема о распределениях оценки по методу наименьших квадратов, величины среднеквадратичного отклонения и величины разности среднеквадратичных отклонений (без доказательства).

Рассмотрим задачу линейной регрессии (9.1)-(9.4), в которой предположение (9.5) заменено более сильным предположением в отношении вектора :

вектор имеет нормальное распределение , ,

(9.10)

где – нулевой вектор порядка и – единичная матрица порядка .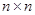

Из (9.2) и (9.4) следует, что наблюдение , тогда из (9.10) следует, что вектор имеет нормальное распределение (как линейное преобразование вектора , имеющего нормальное распределение). Из пункта 1 теоремы 9.3 (в пункте 1 предположение не используется), следует, что и . Таким образом, вектор имеет нормальное распределение с плотностью вероятности:

,

где .

Рассмотрим задачу построения оценки неизвестного вектора параметров по методу максимального правдоподобия. Легко видеть, что функция правдоподобия,

,

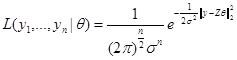принимает наибольшее значение при таком значении вектора параметров , при котором наименьшее значение принимает квадрат нормы . Отсюда следует, что МП-оценка определяется условием:

,

но из (9.2) квадрат нормы совпадает со среднеквадратичным отклонением и наименьшее значение достигается при оценке по методу наименьших квадратов . Отсюда следует, что в задаче нормальной линейной регрессии (9.1)-(9.4), (9.10) оценка по методу наименьших квадратов одновременно является оценкой максимального правдоподобия вектора параметров .