Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Сравнение метода Монте-Карло и квадратурных методов.

Методы приближенного вычисления интегралов, представленные выше, допускают естественное обобщение на кратные интегралы, и как оказывается, при больших кратностях интегралов методы Монте-Карло имеют преимущество над квадратурными методами.

Квадратурные методы используют значения подынтегральной функции в узлах многомерной сетки, поэтому объем вычислений производимых квадратурными методами является величиной порядка , где – кратность интеграла и – постоянная, характеризующая средние вычислительные затраты на вычисление функции в одном узле (и некоторые усредненные затраты, связанные с умножением на вес узла и сложением). Методы Монте-Карло помимо вычисления значения функции требуют вычисления реализаций случайных величин (в частности 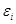), поэтому постоянная, характеризующая вычислительные затраты на одно вычисление значения функции, оказывается больше . Тем не менее, при увеличении кратности увлечение количества суммируемых величин (увеличение происходит в силу требования достижения заданной точности) линейно зависит от , поэтому в результате вычислительные затраты в методах Монте-Карло являются величиной порядка , то есть линейно зависят от .

Экспериментальное сравнение выявляет преимущество квадратурных методов над методами Монте-Карло при небольших кратностях порядка и , однако, при кратностях порядка 8 и больше методы Монте-Карло имеют существенное преимущество над квадратурными методами.