Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Метод получения векторных случайных величин с распределением .

Пусть методом, представленным выше, получены случайные величины 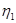, …, , которые имеют распределение и некоррелированы (или коэффициенты корреляции настолько малы, что ими можно пренебречь). Будем считать, что вектор имеет нормальное распределение , где – нулевой вектор порядка и – единичная матрица порядка 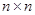. Образуем вектор с помощью линейного преобразования вектора :

,

где – некоторая матрица порядка 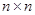. Вектор имеет нормальное распределение, поскольку получен с помощью линейного преобразования вектора , имеющего нормальное распределение. Математическое ожидание :

.

Остается лишь выбрать матрицу таким образом, чтобы дисперсионная матрица вектора оказалась равной заданной матрице . По свойству дисперсионной матрицы:

,

откуда следует, что матрица должна удовлетворять равенству:

.

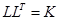Ковариационная матрица всегда симметрична и в некоторых случаях положительно определена, для таких матриц существует матрица , удовлетворяющая 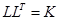, причем матрицу можно сделать нижнетреугольной (для эффективной организации вычислений).

В частности для получения вектора с распределением , где – коэффициент корреляции, , , 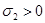достаточно выполнить следующее преобразование:

.