
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вычисление определенных интегралов.
|
|
Пусть  – заданная функция, интегрируемая на отрезке
– заданная функция, интегрируемая на отрезке  , где
, где 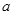 и
и  конечные числа, и требуется приближенно вычислить интеграл:
конечные числа, и требуется приближенно вычислить интеграл:
 .
.
Задача вычисления интеграла с помощью методов статистических испытаний может быть решена двумя способами.
Первый способ: предварительно преобразуем интеграл с помощью замены переменных  к виду:
к виду:
 ,
,
где случайная величина  имеет равномерное распределение
имеет равномерное распределение  . Пусть
. Пусть 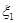 , …,
, …,  – независимые случайные величины с равномерным распределением
– независимые случайные величины с равномерным распределением  , определим величины
, определим величины  , …,
, …,  :
:
 ,
,
легко видеть, что  , тогда:
, тогда:
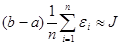 .
.
Второй способ: поскольку  интегрируема, то
интегрируема, то  ограничена на отрезке
ограничена на отрезке  , пусть
, пусть  при
при  . Преобразуем исходный интеграл к виду:
. Преобразуем исходный интеграл к виду:
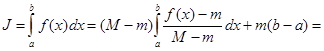

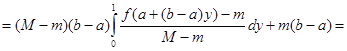
 ,
,
где значения функции  при
при 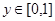 . Пусть
. Пусть 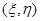 – случайный вектор, в котором
– случайный вектор, в котором  и
и  независимые случайные величины с равномерным распределением
независимые случайные величины с равномерным распределением  , образуем случайную величину
, образуем случайную величину 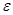 :
:
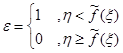 .
.
Заметим, что математическое ожидание  :
:
 .
.
Пусть  , …,
, …,  –
–  пар случайных векторов, в которых каждая случайная величина не зависит от остальных и имеет равномерное распределение
пар случайных векторов, в которых каждая случайная величина не зависит от остальных и имеет равномерное распределение  . Образуем случайные величины
. Образуем случайные величины  , …,
, …,  :
:
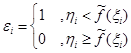 ,
,
тогда,
 ,
,
 .
.
|
|
