
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Постановка задачи построения точечной линейной оценки среднего при разноточных измерениях, метод построения линейной оценки с минимальной дисперсией и свойства коэффициентов.
|
|
Известно, что случайные величины  (
(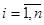 ) имеют вид:
) имеют вид:
 ,
, 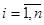
где  неизвестное числовое значение,
неизвестное числовое значение, 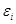 попарно независимые случайные величины с математическим ожиданием
попарно независимые случайные величины с математическим ожиданием  и дисперсией
и дисперсией  , значения
, значения  известны. Требуется построить оценку
известны. Требуется построить оценку 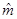 неизвестной величины
неизвестной величины  , такую что
, такую что
1) Оценка 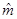 линейная:
линейная:
 ,
,
2) Оценка 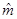 является несмещенной оценкой
является несмещенной оценкой  :
:
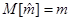
3) Оценка 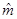 имеет наименьшую дисперсию в классе линейных оценок:
имеет наименьшую дисперсию в классе линейных оценок:
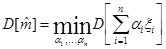 .
.
Легко видеть, что  , тогда:
, тогда:
 .
.
Поскольку 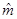 должна быть несмещенной оценкой, то нужно потребовать чтобы
должна быть несмещенной оценкой, то нужно потребовать чтобы  :
:
 .
.
 .
.
Вычислим дисперсию 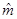 , учитывая, что в силу попарной независимости величин
, учитывая, что в силу попарной независимости величин 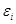 ковариация
ковариация 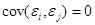 при
при  :
:

 .
.
Таким образом, приходим к задаче минимизации квадратичной формы 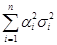 по неизвестным
по неизвестным  при условии, что
при условии, что  . Для решения задачи нахождения условного экстремума воспользуемся методом множителей Лагранжа, функция Лагранжа
. Для решения задачи нахождения условного экстремума воспользуемся методом множителей Лагранжа, функция Лагранжа  имеет вид:
имеет вид:
 .
.
Дифференцируя по  и
и  , получим систему:
, получим систему:




 .
.
Таким образом, искомая оценка 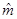 имеет вид:
имеет вид:
 ,
,
при этом дисперсия оценки 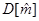 :
:
 .
.
Обозначим  , тогда
, тогда 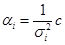 и отсюда становится понятно, что чем меньше
и отсюда становится понятно, что чем меньше  , тем больше коэффициент
, тем больше коэффициент  , то есть чем более «точным» является измерение
, то есть чем более «точным» является измерение  , тем с большим «весом» оно входит в сумму оценки
, тем с большим «весом» оно входит в сумму оценки  . Например, если
. Например, если  -ое измерение «точнее»
-ое измерение «точнее»  -го в 3 раза, то есть
-го в 3 раза, то есть  , тогда
, тогда  , то есть «вес» измерения
, то есть «вес» измерения  в сумме оценки
в сумме оценки 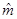 в
в  раз больше «веса» измерения
раз больше «веса» измерения 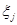 .
.
Функция правдоподобия, функция вклада и информация Фишера. Условия регулярности и свойства функции правдоподобия и функции вклада в условиях регулярности. Теорема о неравенстве Рао-Крамера.
|
|
