Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Определение 2.3.

Статистика 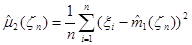называется выборочной дисперсией.

Легко видеть, что оценка 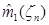является несмещенной, действительно:

.

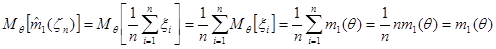Для доказательства состоятельности оценки 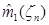может быть использована теорема Хинчина или утверждение 2.1. Заметим, что в случае использования утверждения 2.1 требуется существование дисперсий случайных величин 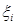, в то время как теорема Хинчина применима даже в тех случаях, когда у случайных величин 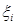дисперсии не существует.

В данном случае величины , , …, 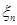образуют выборку, поэтому они независимы, имеют одинаковую функцию распределения, и, следовательно, одинаковое математическое ожидание 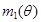, конечность которого гарантируется исходной постановкой рассматриваемой задачи оценки. Таким образом, к совокупности случайных величин , …, 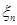при 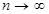применима теорема Хинчина, и поскольку статистика 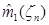есть в точности 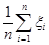получим:

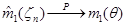, при ,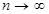

что и означает состоятельность оценки .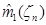

Поскольку оценка 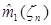является несмещенной, то состоятельность оценки 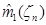может быть доказана с использованием утверждения 2.1, при условии, что дисперсия оценки конечна и стремиться к нулю с ростом . Вычислим непосредственно из определения статистики :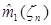

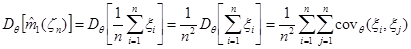
поскольку величины , …, 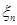образуют выборку, то согласно определению выборки они независимы в совокупности и, следовательно, попарно независимы, так что 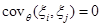при . При 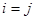, конечно, 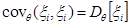, поэтому:

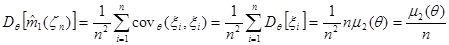
(2.4)

Поскольку 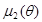предполагается конечной по условию постановки исходной задачи, приведенной в начале пункта, то дисперсия конечна и монотонно стремится к нулю с ростом , поэтому в силу утверждения 2.1 оценка 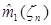является состоятельной.

Исследуем свойства оценки 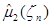, предварительно преобразовав статистику 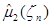к следующему виду:

.

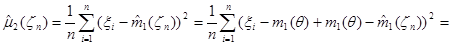
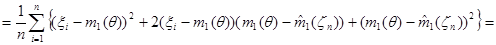
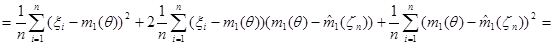
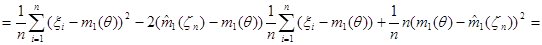
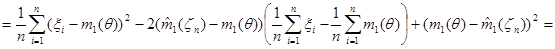
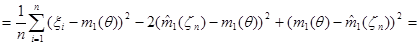
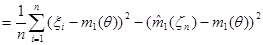Вычислим математическое ожидание :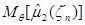

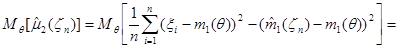
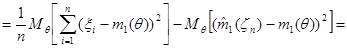
(поскольку , то

)

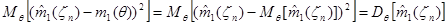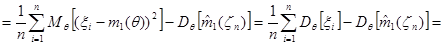
(дисперсия 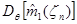была вычислена ранее – соотношение 2.2)

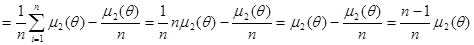
Таким образом,

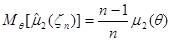
(2.5)

и оценка 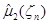оказывается смещенной, но смещение легко исправить, в результате приходим к новой оценке:

.

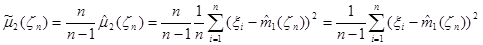Оценка 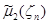является несмещенной, действительно,

.
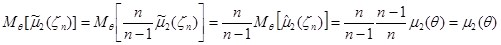