Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Определение 1.13.

Среднеквадратической ошибкой статистики 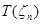, оценивающей величину , называется математическое ожидание квадрата отклонения:

.

В случае несмещенной оценки, , среднеквадратическая ошибка становится равной дисперсии, поэтому для несмещенных оценок критерий наименьшей среднеквадратической ошибки совпадает с уже рассмотренным критерием наименьшей дисперсии.

В более общем случае в рассмотрение вводится функция потерь , которая используется при вычислении функции условного риска :

,

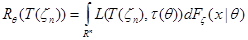где функция распределения выборки . Значения функции используются для сравнения оценок, в частности, если , то функция условного риска есть среднеквадратическая ошибка.

Понятие состоятельной оценки и предельные теоремы, используемые для доказательства состоятельности оценок (теорема Бернулли, теорема Хинчина, неравенство Чебышева и закон больших чисел в форме Чебышева). Утверждение о состоятельности несмещенной оценки с убывающей дисперсией (без доказательства).

Теорема (Бернулли)

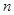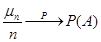Пусть – количество появлений события в независимых испытаниях, тогда последовательность относительных частот сходится по вероятности к вероятности события , при :

, при .

Теорема (Хинчин)

Пусть , , … – последовательность взаимно независимых случайных величин, имеющих одинаковую функцию распределения с конечным математическим ожиданием , тогда последовательность случайных величин 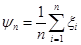сходится по вероятности к , при :

, при .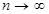

Утверждение (неравенство Чебышева)

Пусть случайная величина имеет конечную дисперсию, , тогда:

.

Теорема (закон больших чисел в форме Чебышева)

Пусть , , … – последовательность взаимно независимых случайных величин, имеющих конечные математические ожидания , , … и конечные дисперсии , , 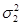… соответственно.

Если,

,

Тогда последовательность арифметических средних случайных величин 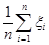сходится по вероятности к арифметическому среднему математических ожиданий при:

, при 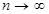.