Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Утверждение 2.1.

Пусть – наблюдения, и статистика 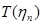является несмещенной оценкой величины , причем дисперсии конечны и стремятся к нулю с ростом :

,

,

,

тогда 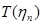является состоятельной оценкой .

Задача точечного оценивания вероятности события, построение оценки и свойства оценки. Задача точечного оценивания значений функции распределения, построение оценки и свойства оценки.

Пусть 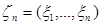выборка из распределения с неизвестным параметром , и некоторое фиксированное числовое значение, требуется построить оценку значения функции распределения – неизвестной величины (неизвестной в силу того, что параметр неизвестен) и исследовать свойства несмещенности и состоятельности построенной оценки.

Предположим, что в качестве оценки неизвестной величины вероятности используется значение эмпирической функции распределения ,

,

где согласно определению эмпирической функции распределения 1.6 функция равна случайной величине количества случайных величин выборки 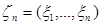меньших . Заметим, что функцию можно представить в виде суммы значений индикаторных функций от случайных величин выборки:

,

где () принимает значение 1 если и 0 в противном случае. Таким образом, каждая величина является случайной величиной, принимающей лишь два значения: 1 с вероятностью и 0 с вероятностью :

.

Поскольку 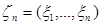выборка из распределения , то в соответствии с определением выборки 1.1, все случайные величины имеют функцию распределения , отсюда следует, что ,

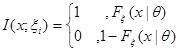
Таким образом, окончательно статистика имеет вид:

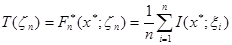
(2.1)

где - случайные величины,

.

Исследуем свойства оценки (2.1), покажем, что статистика (2.1) является несмещенной оценкой , действительно, по свойству математического ожидания,

.

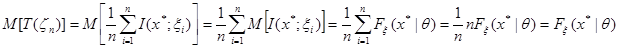Для исследования свойства состоятельности оценки достаточно вспомнить теорему о сходимости по вероятности значений эмпирической функции распределения к значениям при всяком фиксированном . Поскольку оценка в точности совпадает с , то очевидно сходится по вероятности к при и, следовательно, является состоятельной.

Задача точечного оценивания математического ожидания и дисперсии. Понятие о выборочном среднем, выборочной дисперсии и исправленной выборочной. Несмещенность и состоятельность выборочного среднего, выборочной дисперсии и исправленной выборочной дисперсии (без вывода формулы дисперсии выборочной дисперсии).

Пусть 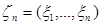выборка из распределения с неизвестным параметром , требуется построить оценки первого начального момента (математического ожидания) 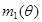и второго центрального момента (дисперсии) 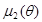(при условии, что указанные моменты конечны):

,

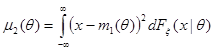
и исследовать свойства построенных оценок.

Для построения оценок воспользуемся определениями моментов, приведенными выше, в которых неизвестную функцию распределения заменим известным «приближением» – эмпирической функцией распределения :

,

.

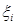Поскольку является ступенчатой функцией, с разрывами величины в точках (), то в результате вычисления интегралов получим следующие статистики:

	(2.2)
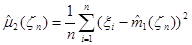
	(2.3)