Автокорреляция остатков

В эконометрических исследованиях часто возникают ситуации, когда дисперсия остатков постоянна, но наблюдается статистическая зависимость остатков эконометрической модели между собой. Это явление называют автокорреляцией остатков.

В общем случае автокорреляция (последовательная корреляция) – это взаимосвязь упорядоченных во времени или в пространстве последовательных элементов соответственно временного или пространственного ряда данных.

На рис.5.5 показана зависимость Y от X, а также линия оцененного по этим данным уравнения парной линейной регрессии. Уже по рисунку видно, что оцененная регрессия не очень хороша: зависимость Y от X явно нелинейна. Если использовать проведенную регрессионную прямую, скажем, для прогнозирования дальнейшей динамики Y, результат будет неудовлетворительным.

Рис.5.5. К вопросу об автокорреляции остатков

Как же можно выразить формально неудовлетворительность полученного уравнения регрессии?

Мы видим, например, на рис.5.5, что в этом случае отклонения от линии регрессии не случайно распределены вокруг нее, а обладают определенной закономерностью. Эта закономерность, в частности, выражается в одинаковом, как правило, знаке каждых двух соседних отклонений. Это может являться следствием:

- неверной спецификации модели (ввиду нелинейного характера связи переменных);

- воздействием какого-то фактора, не включенного в модель в качестве объясняющей переменной. Величина такого неучтенного фактора может менять свою динамику в рассматриваемый период, отклоняясь в достаточно длительные промежутки времени в ту или иную сторону от своего среднего значения. Это, очевидно, может служить причиной длительных устойчивых отклонений зависимой переменной от линии регрессии.

Обе указанные причины свидетельствуют о том, что существует возможность улучшить уравнение регрессии путем оценивания какой-то новой нелинейной формулы или включения некоторой новой объясняющей переменной.

Зависимость, показанная на рис.5.5, очевидно, нелинейна. Но это – крайний случай. Далеко не всегда бывает столь же очевидно, что отклонения от регрессионной прямой имеют неслучайный, закономерный характер. Для оценки степени такой неслучайности необходимо ввести количественную меру.

Итак, одним из основных предполагаемых свойств отклонений наблюдаемых значений от регрессионной формулы является их статистическая независимость между собой.

Мы рассмотрим наиболее простую модель, в которой ошибки образуют так называемый авторегрессионный процесс первого порядка, т.е. когда ошибки зависят только от ошибок предыдущего периода. Применение обычного метода наименьших квадратов в этом случае дает несмещенные и состоятельные оценки параметров, однако можно показать, что оценка дисперсии оказывается смещенной вниз, что может отрицательно сказаться при проверке гипотез о значимости оценок параметров. Образно говоря, МНК рисует более оптимистичную картину, чем есть на самом деле.

Следовательно, последствия автокорреляции состоят в том, что:

- МНК-оценки в случае авторегрессии первого порядка несмещены, состоятельны, но неэффективны;

- оценка дисперсии при использовании МНК является заниженной.

Большинство тестов на наличие автокорреляции в ошибках модели (наиболее широко используется тест Дарбина-Уотсона) используют следующую идею: если корреляция есть у ошибок , то она присутствует и в остатках 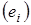, получаемых после применения к модели обычного метода наименьших квадратов.

То есть, поскольку значения ошибок остаются неизвестными ввиду неизвестности истинных значений параметров модели, то проверяется статистическая независимость их аналогов – отклонений . При этом проверяется обычно их некоррелированность (являющаяся необходимым, но недостаточным атрибутом независимости), причем некоррелированность не любых, а соседних величин .

Соседними можно считать:

- соседние во времени значения (в случае временных рядов);

- соседние по возрастанию переменной Х значения (в случае перекрестных выборок).

Для этих величин можно рассчитать, например, коэффициент корреляции (называемый коэффициентом автокорреляции первого порядка) .

“ Первого порядка ” означает, что остатки зависят только от остатков предыдущего периода.

Практически, однако, используют тесно связанную с статистику Дарбина-Уотсона, обозначаемую как DW-статистика или как d‑ статистика, и рассчитываемую по формуле:

. (5.13)

Причем

.