Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Коэффициент детерминации не может служить удовлетворительной мерой качества подгонки при использовании взвешенного МНК. В общем случае может выходить даже за пределы интервала .
|
|
Обобщенный метод наименьших квадратов (метод Эйткена)
Итак, для устранения гетероскедастичности спецификацию исходной модели трансформируют так, чтобы остатки имели постоянную дисперсию. Далее неизвестные параметры трансформированной модели оценивают обычным методом наименьших квадратов.
Если эконометрическая модель содержит только две переменные, то преобразование исходных данных делается так, как описано выше.
Это преобразование значительно усложняется, если строится множественная линейная регрессия.
Поэтому в общем случае для оценивания параметров эконометрической модели с гетероскедастичностью применяют обобщенный метод наименьших квадратов (метод Эйткена), согласно которому оператор оценивания вектора параметров B в матричной форме выглядит так:
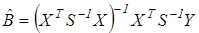, (5.12)
где S – это матрица, с помощью которой преобразуются исходные данные.
В случае гомоскедастичности оценка обобщенного метода наименьших квадратов (5.12) совпадает с оценкой обычного МНК, которую для гомоскедастичной модели в матричной форме получают оператором: 
.
|
|