Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 9
|
|
Составить уравнение эллипса, если известны его эксцентриситет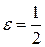 
, фокус 
и уравнение соответствующей директрисы 
.
Решение.
Точка 
принадлежит эллипсу, если отношение расстояний до фокуса и соответствующей директрисы равно 
, т.е. 
.
,
,
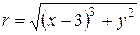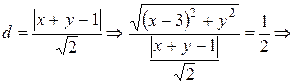
Рисунок 84
.
Ответ.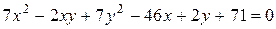 
.
Задача 10
Дано уравнение гиперболы 
. Найти:
а) длины его полуосей;
б) координаты фокусов;
в) эксцентриситет гиперболы;
г) уравнения асимптот и директрис; и нарисовать кривую.
Решение.
Разделив обе части уравнения на 16, приведем уравнение гиперболы к каноническому виду 
: 
.
а) длины его полуосей 
, 
, т.е. 
, 
;
б) координаты фокусов. Используя соотношение 
, находим 
, т.е. 
. Координаты фокусов: 
и 
;
в) эксцентриситет гиперболы. По формуле 
находим 
;
г) уравнения асимптот и
директрис найдем по формулам
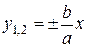и 
:
и 
.
Рисунок 85
|
|