Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 4. Дано уравнение эллипса
|
|
Дано уравнение эллипса 
. Найти:
а) длины его полуосей;
б) координаты фокусов;
в) эксцентриситет эллипса;
г) уравнения директрис и расстояние между ними;
д) точки эллипса, расстояние от которых до левого фокуса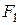 
равно 12.
Решение. Разделив обе части уравнения на 1176 мы получим уравнение эллипса в каноническом виде 
.
а) длины полуосей эллипса 
, 
, т.е. 
, 
.
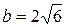б) координаты фокусов. Так как 
, то 
, 
. Следовательно, 
и 
. Рисунок 81
в) эксцентриситет эллипса. Так как 
, то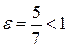 
.
г) уравнения директрис имеют вид 
и 
. Тогда 
, т.е. 
и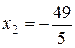 
; расстояние между ними 
.
д) точки эллипса, расстояние от которых до левого фокуса 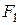равно 12. По формуле 
находим абсциссу точки, расстояние от которой до точки 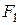равно 12: 
, т.е. 
. Подставляя значение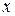 
в уравнение эллипса, найдем ординату этой точки: 
, 
, 
.
Условию задачи удовлетворяет точка 
.
|
|