
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Окружность
|
|
Глава 5 Кривые второго порядка
Линии, определяемые алгебраическими уравнениями второй степени относительно переменных 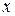 и
и 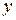 , т.е. уравнениями вида
, т.е. уравнениями вида

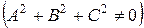 (40)
(40)
называются кривыми второго порядка.
Окружность
Окружностью называется множество всех точек плоскости, удаленных от заданной точки  на одно и тоже расстояние
на одно и тоже расстояние 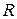 . Точка
. Точка  называется центром, а
называется центром, а 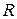 - радиусом окружности.
- радиусом окружности.
В прямоугольной системе координат уравнение окружности имеет вид
 , (41)
, (41)
где  - координаты ее центра. Уравнение (41) называется каноническим уравнением окружности. В частности, если
- координаты ее центра. Уравнение (41) называется каноническим уравнением окружности. В частности, если  ,
,  (т.е. центр окружности совпадает с началом координат), то уравнение (41) имеет вид
(т.е. центр окружности совпадает с началом координат), то уравнение (41) имеет вид
 (42)
(42)
 |
Рисунок 62
Общее уравнение второй степени (40) определяет окружность, если  и
и  .
.
Уравнение второй степени (42) определяет точку при  с координатами
с координатами 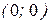 .
.
Уравнение второй степени вида 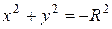 определяет мнимую окружность.
определяет мнимую окружность.
Эллипс
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная (равная  и большая, чем расстояние между фокусами).
и большая, чем расстояние между фокусами).
Каноническое уравнение эллипса:  , (43)
, (43)
где 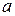 - большая полуось,
- большая полуось,  - большая ось,
- большая ось, 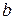 - малая полуось,
- малая полуось,  - малая ось, эллипса. Координаты фокусов:
- малая ось, эллипса. Координаты фокусов:  ,
, 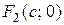 , где с – половина расстояния между фокусами (рисунок 63). Числа
, где с – половина расстояния между фокусами (рисунок 63). Числа 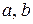 и
и  связаны соотношением
связаны соотношением
 (44)
(44)
Точки  называются вершинами эллипса, точка
называются вершинами эллипса, точка 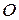 - центром эллипса, расстояния
- центром эллипса, расстояния  и
и  от произвольной точки
от произвольной точки 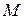 эллипса до его фокусов называются фокальными радиусами этой точки.
эллипса до его фокусов называются фокальными радиусами этой точки.


Рисунок 63 Рисунок 64
Эксцентриситетом  эллипса называется число, равное отношению фокусного расстояния
эллипса называется число, равное отношению фокусного расстояния  (расстояния между фокусами) к длине большой оси
(расстояния между фокусами) к длине большой оси
 :
:  (
( , т.к.
, т.к. 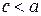 ).
).
Фокальные радиусы определяются формулами:  ,
, 
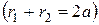 .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Директрисами эллипса называются прямые 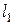 и
и  , перпендикулярные большей оси эллипса симметричные относительно центра, и отстоящие от нее на расстоянии равном
, перпендикулярные большей оси эллипса симметричные относительно центра, и отстоящие от нее на расстоянии равном  : уравнения директрис:
: уравнения директрис:  и
и  (45)
(45)
Замечания: 1) Если  , то уравнение (43) определяет окружность
, то уравнение (43) определяет окружность  ;
;
2) если фокусы эллипса лежат на оси 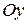 , то эллипс имеет вид: (рисунок 64): В этом случае:
, то эллипс имеет вид: (рисунок 64): В этом случае:  ,
,  ,
,  , уравнения директрис
, уравнения директрис  ;
;
3) уравнение эллипса с центром в точке  , имеет вид
, имеет вид  (рисунок 65).
(рисунок 65).

Рисунок 65
Теорема. Отношение расстояний от любой точки эллипса до фокуса и соответствующей директрисы равно эксцентриситету.
|
|
