Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Гипербола
|
|
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек, называемых фокусами, есть величина постоянная (равная 
, меньшая, чем расстояние между фокусами).
Каноническое уравнение гиперболы: 
, (46)
где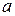 
- действительная полуось, 
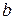- мнимая полуось, и 
называются соответственно действительной и мнимойосями гиперболы. Координаты фокусов: 
, 
, 
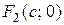- половина расстояния между фокусами (рисунок 66). Числа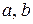 
и связаны соотношением 
(47)
 |
Рисунок 66
Рисунок 66
Точки 
и 
называются вершинами гиперболы, точка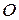 
- центром гиперболы, расстояния 
и 
от произвольной точки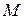 
гиперболы до ее фокусов называются фокальными радиусами этой точки.
Эксцентриситетом 
гиперболы называется число, равное отношению расстояния между фокусами к длине действительной оси.
Число 
(
, т.к. 
) (48)
называется эксцентриситетом гиперболы.
Фокальные радиусы определяются формулами: для точек правой ветви гиперболы: 
, 
; для точек левой ветви: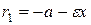 
, 
.
Прямоугольник, центр которого совпадает с точкой 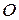, а стороны равны и параллельны осям гиперболы называется основным прямоугольником гиперболы. Диагонали основного прямоугольника гиперболы лежат на двух прямых, называемых асимптотами гиперболы; они определяются уравнениями
(49)
Две прямые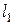 
и 
, перпендикулярные действительной оси гиперболы, расположенные симметрично относительно центра и отстоящие от него на расстоянии, равном 
, называются директрисами гиперболы. Их уравнения: 
и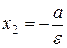 
.
Замечания:
1) Если 
, то гипербола называется равносторонней (равнобочной).
Ее уравнение принимает вид 
.
2) если фокусы гиперболы лежат на оси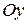 
, то уравнение гиперболы имеет вид: 
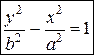(50)
Эксцентриситет этой гиперболы равен 
, асимптоты определяются уравнениями 
, а уравнения директрис 
. Гипербола (50) называется сопряженной гиперболе; если она имеет вид, изображенный на рисунке 67;
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
3) уравнение гиперболы с центром в точке с координатами 
, имеет вид 
(рисунок 68).
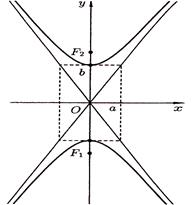
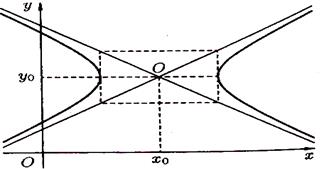
Рисунок 67 Рисунок 68
Теорема. Отношение расстояний от любой точки гиперболы до фокуса и соответствующей директрисы равно эксцентриситету.
|
|