
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Домашнее задание № 5
|
|
1 Найти полуоси, координаты фокусов, эксцентриситет и уравнения директрис эллипса  .
.
Ответ. 5 и 4;  и
и  ;
;  ;
; 
2 Составить каноническое уравнение эллипса если:
а) его большая полуось равна 10 и фокусы есть  ,
,  ;
;
б)  ,
,  ,
,  ;
;
в) задана точка  эллипса и его малая полуось равна 2;
эллипса и его малая полуось равна 2;
г) заданы две точки эллипса  и
и  ;
;
д) эксцентриситет  и заданы фокусы
и заданы фокусы  и
и  ;
;
е) точка  принадлежит эллипсу,
принадлежит эллипсу,  ;
;
к) расстояние между фокусами равно 4, расстояние между директрисами равно 5.
Ответ. а)  ; б)
; б)  ; в)
; в)  ;
;
г) 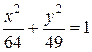 ; е)
; е)  , е)
, е)  ; к)
; к) 
3 Привести уравнение кривой к каноническому виду и изобразить кривую  .
.
Ответ. 
4 Установить и изобразить линию, которая определяется следующими уравнениями: а)  ; б)
; б) 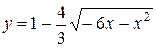 .
.
5 Точка 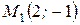 лежит на эллипсе, фокус которого
лежит на эллипсе, фокус которого  , а соответствующая директриса задана уравнением
, а соответствующая директриса задана уравнением  . Составить уравнение этого эллипса.
. Составить уравнение этого эллипса.
Ответ. 
6 Найти канонической уравнение гиперболы с фокусами на оси 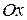 :
:
а)  ,
,  ; б)
; б)  ,
,  ;
;
в)  и уравнения асимптот
и уравнения асимптот  ;
;
г)  и расстояние между директрисами равно
и расстояние между директрисами равно  ;
;
д) проходящей через точки  и
и  .
.
Ответ. а) 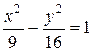 ; б)
; б) 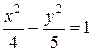 ; в)
; в)  ; г)
; г) 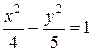 ; д)
; д) 
7 Найти уравнение гиперболы, симметричной относительно осей координат, зная, что ее мнимая полуось равна 2 и гипербола проходит через точку  . Найти расстояние от точки
. Найти расстояние от точки 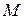 до правого фокуса.
до правого фокуса.
Ответ.  ,
, 
8 Составить уравнения асимптот гиперболы  , построить ее.
, построить ее.
Ответ.  и
и 
9 Написать каноническое уравнение кривой и изобразить кривую  .
.
Ответ. 
10 Точка  лежит на гиперболе, фокус которой
лежит на гиперболе, фокус которой  , а соответствующая директриса дана уравнением
, а соответствующая директриса дана уравнением  . Составить уравнение этой гиперболы.
. Составить уравнение этой гиперболы.
Ответ. 
11 Установить и изобразить линию, которая определяется следующим уравнением: а)  ; б)
; б)  .
.
12 Даны вершина параболы  и уравнение ее директрисы
и уравнение ее директрисы  . Найти фокус
. Найти фокус  этой параболы.
этой параболы.
Ответ. 
13 Установить и изобразить линию, которая определяется уравнением:
а)  ; б)
; б)  .
.
14 Написать каноническое уравнение линии и изобразить ее  .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Ответ. 
|
|
