Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Парабола

Параболой называется множество всех точек плоскости, каждая из которых равноудалена от заданной точки, называемой фокусом и заданной прямой, называемой директрисой.

Каноническое уравнение параболы имеет вид , (51)

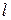где число , равное расстоянию от фокуса до директрисы , называется параметром параболы. Координаты фокуса 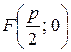. Точка называется вершиной параболы, длина отрезка - фокальный радиус точки 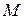, ось 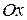- ось симметрии параболы.

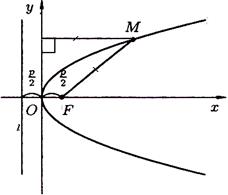
Рисунок 69 Рисунок 70

Уравнение директрисы 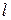параболы имеет вид ;

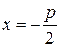фокальный радиус вычисляется по формуле .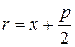

В прямоугольной системе координат парабола, заданная каноническим уравнением , расположена так, как указано на рисунке 69.

Замечания.

1) Парабола, симметричная относительно оси 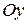и проходящая через точку (рисунок 70), имеет уравнение (52)

Уравнение директрисы: , фокальный радиус точки 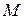параболы .

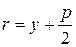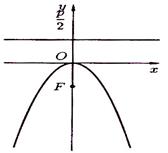
Рисунок 71 Рисунок 72

(53) (54)

3) На рисунках 73 – 76 приведены графики парабол с осями симметрии, параллельными координатным осям.

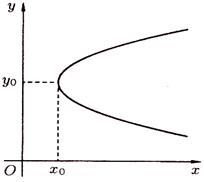
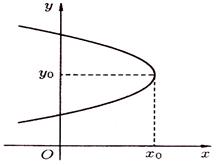
Рисунок 73 Рисунок 74

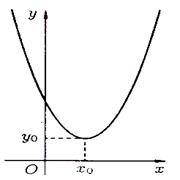
Рисунок 75 Рисунок 76