Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Первый признак подобия

Теорема. Если два угла одного треугольника соответ­ственно равны двум углам другого, то такие треугольники подобны.

Доказательство

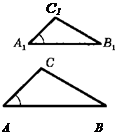
Пусть ∆ АВС и ∆ А₁В₁С₁ — два треугольника, у которых ∠ А=∠ А₁ ∠ В=∠ В₁ (рис. 5). Докажем, что ∆ АВС ~ ∆ A₁B₁C₁.

По теореме о сумме углов тре­угольника ∠ С = 180° - ∠ А - ∠ В, ∠ С₁ =180° - ∠ А₁ - ∠ B₁ и, значит, ∠ С=∠ С₁. Таким об­разом, углы треугольника АВС соответ­ственно равны углам треугольника А₁В₁С₁.

Докажем, что стороны треуголь­ника АВС пропорциональны сходственным сторонам треугольника А₁В₁С₁. Так как ∠ А = ∠ А₁ и ∠ С=∠ С₁, то

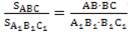
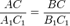
Из этих равенств следует, что. Аналогично, используя ра­венства ∠ А=∠ А₁ ∠ В=∠ В₁, получаем.

Итак, стороны треугольника АВС пропорциональны сходственным сторонам треугольника А₁В₁С₁. Теорема доказана.

Второй признак подобия треугольников

Теорема. Если две стороны одного треугольника про­порциональны двум сторонам другого тре­угольника и углы, заключенные между этими сторонами, равны, то такие треуголь­ники подобны.

Доказательство

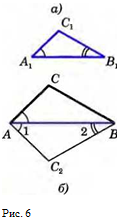Рассмотрим два треугольника АВС и A₁B₁C₁, у которых, ∠ А = ∠ А₁ (рис. 6, а). Докажем, что ∆ АВС ~ ∆ A₁B₁C₁. Для этого, учитывая пер­вый признак подобия треугольников, доста­точно доказать, что ∠ В=∠ В1.

Рассмотрим треугольник АВС₂, у которого ∠ 1 = ∠ А₁, ∠ 2 = ∠ В₁ (рис. 6, б). Треугольники АВС₂ и А₁В₁С₁ подобны по первому признаку подобия треугольников, поэтому

.С другой стороны, по условию.

Из этих двух ра­венств получаем АС=АС₂.

Треугольники АВС и АВС₂ равны по двум сторонам и углу между ними (АВ — общая сторона, АС=АС₂ и ∠ А=∠ 1, по­скольку ∠ А—∠ А₁ и ∠ 1 = ∠ А₁). Отсюда сле­дует, что ∠ В=∠ 2, а так как ∠ 2 = ∠ В₁ то ∠ В = ∠ В₁. Теорема доказана.