
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Движение
|
|
При k=1 преобразование подобия сохраняет расстояния, т.е. является движением. Следовательно, движение – частичный случай преобразования подобия.

 Примерами движений плоскости являются осевая и центральная симметрия, параллельный перенос, поворот. Как пример, напомним определение параллельного переноса.
Примерами движений плоскости являются осевая и центральная симметрия, параллельный перенос, поворот. Как пример, напомним определение параллельного переноса.
Пусть  - некоторый вектор плоскости α. Геометрическое преобразование, переводящее каждую точку
- некоторый вектор плоскости α. Геометрическое преобразование, переводящее каждую точку 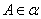 в такую точку
в такую точку  , что
, что  (рис. 3), называется параллельным переносом на вектор
(рис. 3), называется параллельным переносом на вектор  . Параллельный перенос является движением: если точки
. Параллельный перенос является движением: если точки 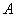 и
и  переходят в
переходят в  и
и 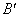 , т.е.
, т.е.  ,
,  , то
, то  , и потому
, и потому 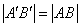 .
.
Свойства движений:
1) Движение переводит прямую в прямые, а параллельные прямые – в параллельные прямые.
2) Движение преводит полуплоскость с границей a в полуплоскость с границей a ', где a ' – образ прямой a.
3) Движение сохраняет простое отношение трёх точек прямой.
4) Движение сохраняет отношение «Лежать между».
5) Движение переводит отрезок AB в отрезок A'B', где A' и B' – образы точек A и B. При этом середина отрезка AB переходит в середину отрезка A'B'.
6) Движение переводит луч в луч, а угол в угол.
7) Движение переводит угол в равный ему угол.
8) Движение переводит взаимно перпендикулярные прямые во взаимно перпендикулярные прямые.
|
|
