Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Тема 6. Автоколебательные системы с одной степенью свободы

Конструкция, которая генерирует колебания без внешнего воздействия, называется автоколебательной системой. Автоколебательные системы являются автономными (на них нет воздействия), а также активными (генерируют энергию). Колебательный процесс всегда периодический, а это значит, что полная колебательная энергия системы N = T + V (здесь Т - кинетическая энергия) является периодической функцией времени, т. е. N (t + nT) = N (t) (здесь Т - период колебаний). С другой стороны, в системе действует диссипация, тогда из известного уравнения (1.35)

,

где F (t) - функция, характеризующая диссипативные свойства системы, причём для диссипативных систем F (t) > 0. Также для F (t), исходя из предыдущего равенства и периодичности функции N, справедливо

.

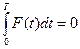(6.1)

Но так как для автономных диссипативных систем функция F (t) всегда положительна (а интеграл от всегда положительной функции не может быть равен нулю), то это значит, что в автономных диссипативных системах устойчивые автоколебания невозможны, т. е. всегда требуется подкачка энергии. Например, если рассмотреть простейший последовательный RLC колебательный контур, то функция диссипации будет F (t) = R (i) i ². Таким образом, чтобы возникли устойчивые колебания, необходимо, чтобы значение R (i) хотя бы на каких-то участках было отрицательным.