Энергия системы зарядов

Система заряженных тел обладает потенциальной энер­гией, так как силы, с которыми они взаимодействуют, являются консервативными. Рассмотрим систему, состоящую из двух точечных зарядов q₁ и q₂, находящихся на расстоянии r₁₂ друг от друга. При удалении одного из зарядов на бесконечность силы взаимодействия между ними уменьшаются до нуля. При сближении зарядов на расстояние r₁₂ необходимо совершить работу, которая идет на увеличение или на уменьшение (в зависимости от относительного знака зарядов) потенциальной энергии системы зарядов.

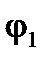Пусть заряд q1 приближается к заряду q2 из бесконечности на расстояние r12. Работа по его перемещению равна , где - потенциал создаваемый зарядом q2, или . С другой стороны, если заряд q2 приближается из бесконечности к заряду q1 на тоже самое расстояние, то при этом совершается работа , где - потенциал, созданный не подвижным зарядом q1, или . Работы получились одинаковыми, поскольку начальное и конечное расположение зарядов одинаково. Каждая из работ А1 и А2 равна энергии взаимодействия двух зарядов

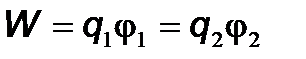
или в симметричной форме

.

Если добавить к данной системе еще один заряд q₃, перенесенный из бесконечности, то работа A₃, затрачиваемая при таком перемещении, равна , где - потенциал, создаваемый зарядами q₁ и q₂ в точке, где находится заряд q₃, или

.

Энергия взаимодействия трех точечных зарядов W равна сумме работ А₁, А₂ и А₃:

,

или в симметричной форме:

.

Таким образом, потенциальная энергия системы из N зарядов опре­деляется выражением:

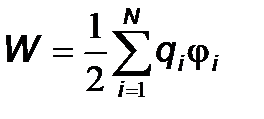, (4. 1)

где 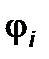- потенциал, создаваемый всеми зарядами, кроме i - го, в точке, где находится i- й заряд.