Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Неоднородные диэлектрики. Граничные условия

Бесконечно протяженных однородных диэлектриков в природе не существует. В общем случае плотность, температура диэлектрика могут плавно меняться от точки к точке. Для таких диэлектриков остается справедливым уравнение (2. 9), но направление вектора D, как правило не совпадает с направлением вектора Е0. На практике часто приходится иметь дело с образцами, состоящими из нескольких однородных диэлектриков, разделенных резкой границей. В этом случае при определении напряженности электрического поля Е и вектора электрического смещения D следует учитывать соответствующие граничные условия.

Выбирается небольшой участок раздела двух диэлектриков, который в пределе может считаться плоским. Граничные условия записываются

отдельно для нормальных и тангенциальных составляющих векторов Е и D.

Граничные условия для нормальных составляющих определяются по теореме Гаусса. Найдем поток вектора D через поверхность параллелепипеда (рис. 2.11) вблизи границы двух диэлектриков с диэлектрическими проницаемостями ε 1 и ε 2. Согласно теореме Гаусса для диэлектриков (2. 8) и с учетом направления внешних dS, поток будет равен

,

где q – сумма свободных зарядов внутри выбранной поверхности интегрирования. Если на поверхности раздела диэлектриков нет специально нанесенных свободных зарядов, то

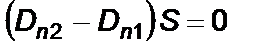и .

Таким образом, нормальная составляющая вектора электрического смещения на любой поверхности, не несущей поверхностного заряда, непрерывна.

Можно показать, что нормальная составляющая вектора электрического поля Е на поверхности раздела диэлектриков терпит разрыв:

.

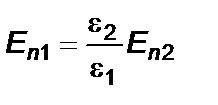Граничные условия для тангенциальных составляющих определяются из требования:

.

Интегрируя по замкнутому прямоугольному контуру вблизи границы раздела двух диэлектриков (рис. 2.12), получим

,

из которого следует

.

Тангенциальная составляющая вектора напряженности электрического поля на поверхности раздела диэлектриков всегда непрерывна. В свою очередь, тангенциальная составляющая вектора электрического смещения на границе раздела диэлектриков терпит разрыв:

.

Вопросы и качественные задачи

1. Пластину из диэлектрика внесли в заряженный плоский конденсатор. Получится ли два разноименно заряженных куска диэлектрика, если распилить пластину параллельно обкладкам конденсатора? Сопоставьте результаты такого опыта для диэлектрика и проводника.

2. Что можно сказать о внутреннем устройстве диэлектрика, если известно, что его диэлектрическая проницаемость значительно изменяется с температурой? Что о нем можно сказать, если эта зависимость очень слабая?

3. Положительный и отрицательный точечные заряды притягиваются с некоторой силой. Как изменится сила, действующая на каждый из этих зарядов, если поместить между зарядами шар из этого диэлектрика?