Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Энергия заряженного конденсатора

Энергию заряженного конденсатора можно вычислить следующим образом. Обкладки конденсатора разбиваются на малые участки, заряд которых принимается за точечный. Учтем, что обкладки являются эквипотенциальными поверх­ностями. Пусть первая обкладка имеет заряд q потенциал , а вторая имеет заряд -q и потенциал . Тогда энергия первой обкладки, согласно (4.1), равна 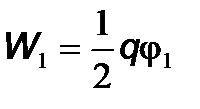, а энергия второй равна .

Полная энергия заряженного конденсатора равна

или, с учетом (3. 6)

. (4. 2)

С помощью данного выражения можно найти силу, с кото­рой обкладки плоского конденсатора притягиваются друг к другу. Для этого предположим, что расстояние между пласти­нами меняется, и в формулу (4. 2) подставим выражение (3. 7), обозначив переменный зазор между обкладками через х (вместо d):

. (4.3)

Будем считать заряд на обкладках постоянным (конден­сатор отключен от источника напряжения) и, воспользовав­шись соотношением, связывающим энергию и силу, получим

. (4. 4)

В формуле (4. 4) знак минус указывает на то, что сила стремится уменьшить расстояние x между обкладками и является силой притяжения.