Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Проводники в электрическом поле

При внесении незаряженного проводника в электриче­ское поле (рис. 3.2) свободные электроны проводника пере­мещаются против направления линий напряженности внешнего электрического поля Е0. Что приводит к образова­нию на одной стороне проводника избытка отрицательных зарядов, на другой - избытка положительных зарядов. Это явление называется электростатической индукцией.

Поле Е′ индуцированных зарядов q′ (появившихся на поверхности проводника) полностью компенсируют внутри проводника внешнее поле Е0. В противном случае, внутри проводника происходил бы перенос электрических зарядов.

Если внутри проводника имеется полость, то при равно­весном распределении зарядов по поверхности проводника внут­ри полости поле также отсутству­ет. На свойстве проводников экранировать (не пропускать внутрь области, окруженной про­водником) внешние поля основывается защита от действия внешних электрических полей.

Замкнутый полый проводник экранирует полость внутри себя только от внешних полей (рис. 3.3).

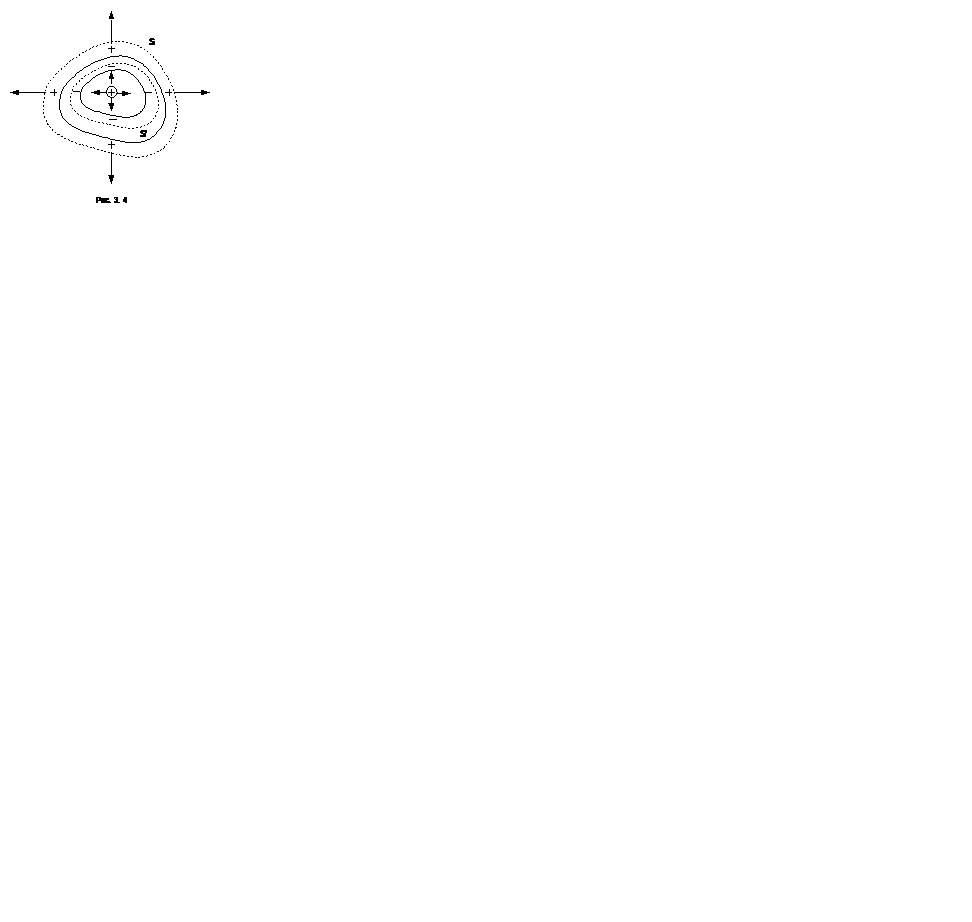
Если же заряды находят­ся внутри полости (рис. 3.4), то они вызывают появление ин­дукционных зарядов и на внут­ренней (-q′), и на внешней (q′) поверхности проводника. При этом внутри проводника поле равно нулю, а внутри полости отлично от нуля.

Используя теорему Гаусса (в качестве поверхности интегрирования вы­бирается поверхность S´, проходящая внутри оболочки), можно доказать, что на внутренней поверхности оболочки образуется заряд, равный по абсолютной величине заряду внутри полости и противоположный ему по знаку ().

Для доказательства существования электрического поля во внешнем пространстве также воспользуемся теоремой ремой Гаусса. В этом случае поверхность интегрирования S (рис. 3.4), окружает оболочку. Полный заряд в объеме, ограниченном этой замкнутой поверхностью, равен заряду q внутри плоскости. Следовательно, согласно (1.15) имеем

, (3. 3)

т. е. напряженность поля не равна нулю в окружающем оболочку пространстве.

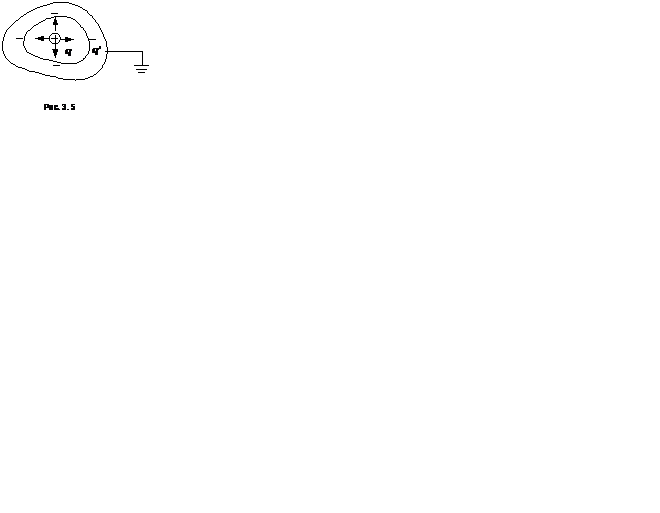
Заземлим оболочку, т. е. соединим её проводником с Землей. В этом случае все заряды с внешней поверхности уйдут на Землю, а на внутренней поверхности останутся (рис. 3. 5).

Согласно, теореме Гаусса уравнение (3. 3) примет вид

,

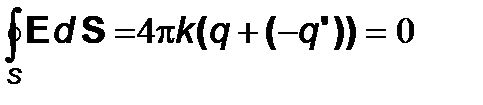т. е. напряженность поля Е во внешнем пространстве, окружающем оболочку, равна нулю. Таким образом, заземленная замкнутая металлическая оболочка экранирует внешнее пространство от зарядов, расположенных в объёме, окруженном этой оболочкой. Незаземленная оболочка такой экранировки не создает.

§ 3. 3. Электроемкость. Конденсаторы

Увеличение заряда на проводнике, согласно (3. 1), пропорционально увеличению напряженности электрического поля. Это, в свою очередь, приводит к возрастанию работы по переносу заряда из бесконечности на поверхность проводника в тоже самое число раз. Согласно (1. 33), данная работа равна потенциалу проводника:

.

Следовательно, потенциал уединённого проводника пропорционален его заряду:

.

Коэффициент пропорциональности С между зарядом называется электроемкостью (или емкостью) проводника. Таким образом, емкостью уединённого проводника называется физическая величина равная заряду, сообщение которого проводнику повышает его потенциал на единицу:

. (3. 4)

Емкость характеризует способность проводника накапливать заряды. Емкость проводника зависит от его размеров и формы. В этом можно убедиться, если рассчитать емкость уединенной проводящей сферы. Из формулы (1. 41) при R2 стремящемся к бесконечности и R1=R следует, что потенциал сферы радиусом R равен

_,

тогда емкость данного шара равна

, (3. 5)

т. е. емкость пропорциональна радиусу сферы.

На практике часто требуются проводники с большой емкостью, способные при небольшом потенциале накапливать значительный заряд. Увеличение емкости проводника можно достигнуть, не только увеличивая его размеры, но и приблизив к нему другой проводник или диэлектрик.

Устройства, основанные на свойстве проводников увеличивать свою емкость в присутствии других проводников, называются конденсаторами.

Конденсатор состоит из двух проводников, заряженных разноименными, равными по абсолютной величине зарядами. Проводники должны иметь такую геометрическую форму и должны быть так расположены друг относительно друга так, чтобы электрическое поле, созданное этими проводниками, было сосредоточено между ними. Проводники, которые образуют конденсатор, называются обкладками. Зарядом конденсатора называется абсолютная величина заряда одной из обкладок конденсатора.

Емкостью конденсатора называется отношение заряда конденсатора q к напряжению между его обкладками:

. (3. 6)

Примерами конденсаторов могут служить плоский конденсатор (рис. 3. 6) и сферический (3. 7).

Емкость плоского конденсатора можно вычислить, считая, что расстояние между обкладками d много меньше их линейных размеров. В этом случае можно считать, что поле сосредоточено внутри конденсатора и напряжение между его обкладками определяется формулой (1. 39). Тогда, . С учетом того, что и 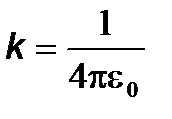, окончательно имеем

, (3. 7)

где S – площадь обкладки конденсатора. Если между обкладками конденсатора имеется диэлектрик с диэлектрической проницаемостью , то формула (3. 7) примет вид:

. (3. 8)

Емкость феерического конденсатора с диэлектриком между обкладками, с учетом формул (3. 6) и (1. 41), вычисляется так , (3. 9)

где R₁ – радиус внутренней обкладки, R₂ – радиус внешней обкладки.

Вопросы и качественные задачи

1. Положительный и отрицательный точечные заряды притягиваются с некоторой силой. Как изменится сила, действующая на каждый из этих зарядов, если поместить между зарядами шар из этого диэлектрика?

2. Как, имея отрицательный заряженный проводник, зарядить положительно другой проводник, не меняя заряд первого?

3. Два металлических шара одинакового радиуса расположены на небольшом расстоянии друг от друга. Одинакова ли будет величина силы электрического взаимодействия шаров в случаях, когда они заряжены одноименно и разноименно?

4. На рисунке показаны силовые линии трех электрических полей. Как будет вести себя металлический шарик, помещенный в каждое из этих полей? Почему?

5. Внутри проводящей незаряженной, но заземленной сферы помещен положительный заряд q. Каково будет распределение зарядов на сфере? Какова величина заряда, индуцированного на ней? Нарисуйте картину силовых линий. Как изменится эта картина, если сферу не заземлять?

6. Заряженный металлический шар присоединен к электрометру. Как будут меняться показания электрометра, если шар подносить близко к проводящим заземленным предметам? Почему?

7. Емкость плоского конденсатора вычисляется по формуле . Будет ли емкость стремиться к нулю, если расстояние между пластинами увеличивать до бесконечности?

8. В середине плоского конденсатора поместили тонкую металлическую пластину. Как изменится емкость конденсатора? Как она изменится, если пластину соединить проволокой с одной из обкладок? Если внести в конденсатор пластину из диэлектрика с и толщиной, равной половине расстояния между обкладками?

9. Обкладки плоского воздушного конденсатора присоединены к аккумулятору. Уменьшится ли напряженность поля в конденсаторе, если поместить его в непроводящую жидкость с диэлектрической проницаемостью ε?

10. Плоский конденсатор заряжается от батареи, которая затем отключается. Между обкладками помещается пластина из диэлектрика. Как изменится заряд, разность потенциалов между обкладками, напряженность поля? Рассмотреть те же вопросы в случае, если батарея не отключается

.