Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Электрическое смещение. Теорема Гаусса для диэлектриков

Рассмотрим однородный и изотропный диэлектрик в электрическом поле Е0, созданным свободными электрическими зарядами q, и поставим задачу рассчитать электрическое поле Е в диэлектрике, например, в произвольной точке А (рис. 2.8). Воспользуемся теоремой Гаусса:

или

, (2. 7)

где (q +q/) – алгебраическая сумма свободных и поляризационных зарядов, охватываемых поверхностью S.

Величина поляризационных зарядов q/ заранее не известна, поэтому в уравнение (2. 7) их надо исключить. Для этого сложим уравнения (2. 6) и (2. 7), и получим

,

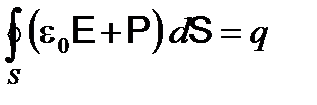или

, (2. 8)

где

. (2. 9)

Вектор D называется вектор электрического смещения или вектор электрической индукции. Воспользуемся уравнением (2. 2) для Р и получим, что

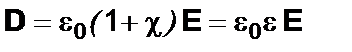, (2. 10)

где коэффициент называется диэлектрической проницаемостью среды.

Величина e > 1 и определяется теми же физическими параметрами, что и диэлектрическая восприимчивость c.

Уравнение (2. 8) выражает теорему Гаусса для диэлектриков: поток вектора электрического смещения через любую замкнутую поверхность S равен алгебраической сумме свободных зарядов, охватываемых этой поверхностью. Если распределение свободных зарядов внутри этой поверхности характеризуется объемной плотностью r, то уравнение (2. 8) можно записать так

. (2. 11)

Таким образом, для решения задачи, поставленной в начале данного параграфа, можно воспользоваться теоремой Гаусса (2. 8 или 2. 11) и определить численное значение вектора D. Затем, зная диэлектрическую проницаемость, из уравнения (2. 10) рассчитать величину напряженности Е в данной точке диэлектрика.В частном случае (рис. 2.9), когда пространство между заряженными бесконечными параллельными металлическими пластинами полностью заполнено однородным изотропным диэлектриком, имеет место соотношение

,

т. е. вектор D с точностью до ε ₀ совпадает с электрическим полем Е ₀, созданным распределением свободных зарядов с плотностью s на данных плоскостях в отсутствии диэлектрика между ними. Соотношение имеет место для бесконечных, однородных и изотропных диэлектриков. В общем случае (рис. 2.10), когда границы диэлектрика не параллельны заряженным плоскостям, вектор D не параллелен Е ₀.

Поле вектора D можно графически изобразить линиями электрического смещения, которые определяются аналогично линиям напряженности электрического поля.