Потенциалы некоторых полей

Потенциал поля точечного заряда. Рассмотрим в данном поле некоторую точку, находящуюся на расстоянии r от заряда q. Помещенный в эту точку заряд q0, обладает потенциальной энергией, которая рассчитывается по формуле (1. 29). Согласно определению потенциала (1. 30), имеем:

. (1. 36)

Такую же формулу можно получить, используя уравнение (1. 33) и проводя интегрирование вдоль линии напряженности (разность потенциалов не зависит от формы пути) от r (точка с потенциалом j) до бесконечности (j¥ =0):

или .

Знак потенциала, как следует из (1. 36), определяется знаком заряда, создающего поле в данной точке.

Потенциал поля системы точечных зарядов по принципу суперпозиции равен алгебраической сумме потенциалов, создаваемых в рассматриваемой точке каждым из зарядов:

, (1. 37)

где r _i- расстояние от заряда q _i.

Разность потенциалов (напряжение) в поле, созданном двумя заряженными плоскостями (рис. 1.10). Выберем произвольную точку, удаленную на расстоянии x от положительно заряженной плоскости. Воспользуемся уравнениями (1. 33) и (1. 21):

. (1. 38)

Напряжение между плоскостями U₀ равно

, (1. 39)

где d – расстояние между пластинами. Поэтому также

. (1. 40)

Таким образом, в данном поле напряжение изменяется с расстоянием по линейному закону.

Напряжение между двумя заряженными (q и -q) концентрическими сферами с радиусами R1 (внутренняя) и R2 (внешняя). Напряжение между внутренней сферой (считаем, что она заряжена положительно) и какой-либо точкой, удаленной на расстояние r < R2 от центра сфер, определим, используя уравнения (1. 33) и (1. 22):

,

откуда напряжение между сферами

. (1. 41)

Вопросы и качественные задачи

1. Какие частицы обычно перераспределяются в пространстве, когда тело заряжается отрицательно? Положительно?

2. а) Можно ли зарядить тело зарядом Кл? Кл?

б) Можно ли равномерно зарядить макроскопическое тело, сообщив ему заряд Кл? 1 Кл?

3. Можно ли считать заряд ядра в атоме точечным? Почему?

4.Является ли электрическое поле просто удобным способом описания электрических явлений или оно реально существует?

5. Является ли в общем случае силовая линия траекторией заряда в поле?

6. Могут ли силовые линии электрического поля пересекаться?

7. Поток вектора напряженности электрического поля, созданного системой зарядов через некоторую замкнутую поверхность, содержащую точку А, равен нулю. Можно ли утверждать, что на заряд помещенный в эту точку силы не действуют?

8. В начало координат помещен положительный заряд , а положительный заряд 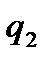перемещается из бесконечности в точку, отстоящую на расстоянии r от . Какова величина энергии, которую необходимо затратить? Какова эта энергия, если заряд отрицательный?

9. Как будут двигаться в поле положительный и отрицательный заряды: от точки с низким потенциалом к точке с высоким потенциалом или наоборот