Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Связь между напряжённостью и потенциалом

Общее выражение для разности потенциалов можно получить, разделив уравнение (1. 26) на q₀:

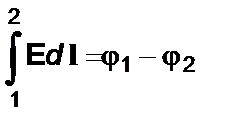. (1. 33)

Из уравнения (1. 33) следует, что или

,

откуда компоненты вектора Е равны: 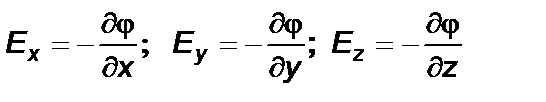, (1. 34)

и

.

Указанная процедура дифференцирования потенциала носит название нахождения градиента потенциала и обозначается как grad или Ñ. Таким образом, напряженность электрического поля в данной точке равна взятому со знаком минус градиенту потенциала поля в той же точке:

. (1. 35)

Вектор gradj всегда направлен в сторону наиболее быстрого возрастания потенциала и показывает, как меняется потенциал поля на единицу длины. В уравнении (1. 35) знак минус означает, что вектор Е всегда направлен в сторону убывания потенциала.

Для графического представления электрического поля вводят, наряду с линиями напряженности, эквипотенциальные поверхности, т.е. поверхности равного потенциала, которые определяются уравнениями На плоскости эти поверхности вырождаются в эквипотенциальные линии. Между двумя точками эквипотенциальной поверхности разность потенциалов равна нулю, поэтому из уравнения (1. 33) следует, что скалярное произведение .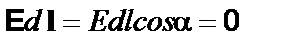

При Е ¹ 0 и dl ¹ 0 должно быть cosa=0, т.е. . Следовательно, эквипотенциальные поверхности всегда перпендикулярны к линиям напряженности (рис. 1.14).

В заключении данного параграфа отметим, что согласно формулам (1. 34), напряженность поля можно измерять в вольтах на метр.