Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Работа сил электрического поля. Циркуляция вектора напряженности

При перемещении зарядов в электрическом поле силы, приложенные к зарядам, совершают работу. Выясним, от чего зависит эта работа. Рассмотрим положительный точечный заряд q0, который перемещается в поле заряда q из точки 1 в точку 2 (рис. 1.12). Для того, чтобы определить работу на всем конечном перемещении 1 - 2, разобьем его на бесконечно малые перемещения dl. Элементарная работ, совершаемая на данном перемещении силой Кулона F, равна

,

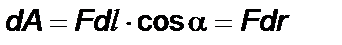где dr – элементарное изменение расстояния между зарядами (длины радиус-вектора r). Полная работа на пути 1 - 2 равна

,

взяв данный интеграл, получим

. 1. 24)

Из уравнения (1. 24) следует, что работа в электрическом поле не зависит от формы пути и определяется только относительными положениями зарядов q и q0 в начале и конце пути. Отсюда, в частности, следует, что работа по перемещению заряда q0 по замкнутому контуру равна нулю. Следовательно, электрическое поле является потенциальным. Условие потенциальности поля можно записать в другой форме. Очевидно, что

,

где Е – вектор поля, создаваемого зарядом q (рис. 1.12). Так как работа по замкнутому контуру L , то

. (1. 25)

Выражение называется циркуляцией вектора напряженности по контуру L. (рис. 1.13).

Таким образом, условие потенциальности электрического поля неподвижных зарядов выражается уравнением (1. 25): циркуляция вектора напряженности по любому замкнутому контуру равна нулю.

Подчеркнем, что уравнение (1. 25) несправедливо, если заряды, создающие поле, движутся.