Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Применение теоремы Гаусса для расчета электрических полей

Практический интерес представляют поля, созданные длинной равномерно заряженной проволокой (цилиндром) радиусом R, бесконечной плоской пластины из металла или диэлектрика, сферической поверхности и диэлектрическим шаром.

Так как заряженные тела содержат весьма большое количество элементарных зарядов, то распределение заряда на них можно считать непрерывным. Это позволяет ввести понятие плотности электрического заряда:

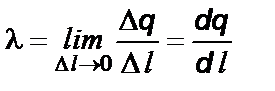, (1. 16)

где l – линейная плотность заряда, D l – элемент длины заряженной проволоки,

D q – элементарное количество заряда, приходящего на D l;

, (1. 17)

где s – поверхностная плотность заряда, D S – элемент поверхности, на котором имеется заряд D q;

, (1. 18)

где r – объемная плотность заряда, D V – элемент объема, содержащий заряд D q.

Теорема Гаусса позволяет рассчитать напряженности полей, создаваемые выше перечисленными заряженными телами.

Поле равномерно заряженной с плотностью t бесконечно длинной проволоки радиуса R (рис. 1.8). В силу симметрии линии напряженности данного поля направлены по нормалям к боковой поверхности проволоки (по радиусам) и на одинаковых расстояниях от нее напряженность поля одинакова по модулю (в противном случае равновесие зарядов на проволоке будет нарушено). Поэтому поверхность интегрирования S удобнее всего выбрать в виде коаксиального цилиндра радиусом r и высотой l, при этомпоток через основание отсутствует. Таким образом

,

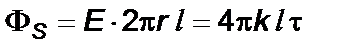где – заряд, охватываемый поверхностью S. Откуда

. (1. 19)

Согласно (1. 19), поле бесконечно длинной проволоки (провода) с равномерной плотностью заряда l обратно пропорционально расстоянию от проволоки. На поверхности проволоки имеем:

.

Поле равномерно заряженной с плотностью s бесконечной плоскости. Из соображений симметрии, очевидно, что линии напряженности данного поля направлены перпендикулярно к плоскости. В качестве поверхности интегрирования S выберем цилиндрическую поверхность с образующими, перпендикулярными к плоскости, и основаниями площадью DS параллельными ей (рис. 1.9). Поток поля через боковую поверхность равен нулю (линии напряженности параллельны боковой поверхности). Поток через основания цилиндрической поверхности по теореме Гаусса равен

,

откуда напряженность поля заряженной плоскости равна

. (1. 20)

Таким образом, поле заряженной бесконечной плоскости однородно, т.е. во всех точках поля вектор напряженности имеет одинаковое направление и одинаковую величину.

Поле двух параллельных разноименно заряженных с поверхностной плотностью s бесконечных плоскостей. Из рис. 1.10 видно, что напряженность поля слева от положительно заряженной плоскости и справа от отрицательно заряженной, в силу принципа суперпозиции, равна нулю (поле отсутствует). Поле в пространстве между плоскостями равно

,

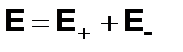где Е ₊ и Е _- – напряженности полей, создаваемые положительно и отрицательно заряженными плоскостями, или

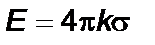. (1.21)

Таким образом, поле между плоскостями является однородным.

Поле заряженной с поверхностной плотностью s сферы радиуса R.

Поле заряженной сферической поверхности обладает центральной симметрией, т.е. направление вектора Е совпадает с направлением радиуса r (рис. 1.11). Согласно теореме Гаусса, напряженность поля внутри сферы Е=0, так как внутри сферы нет зарядов. Для расчета поля вне сферы в качестве поверхности интегрирования выберем коаксиальную сферическую поверхность S радиуса r > R. По теореме (1. 15) имеем . Откуда

. (1. 22)

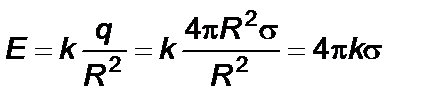. (23)