Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Теорема Гаусса

Для наглядного описания электрического поля используется метод линий напряженности (силовых линий). В каждой точке пространства касательная к линии напряженности сов- падает по направлению с вектором напряженности электрического поля (рис. 1.4). Линии напряженности электрического поля неподвижных зарядов (электростатического поля) начинаются на положительных и оканчиваются на отрицательных зарядах, либо уходят в бесконечность (рис. 1.5).

По густоте линий напряженности можно судить о величине Е. Число линий, пронизывающих единицу поверхности площадки (DS=1 м2), перпендикулярной к линиям напряженности, равно численному значению Е в данной области пространства.

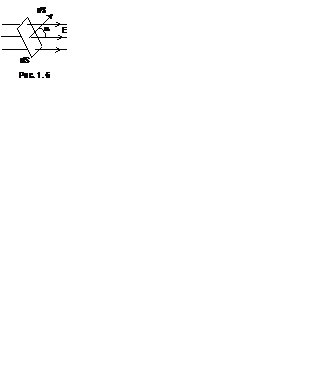Основной задачей электростатики является расчет электрического поля (Е) по заданному распределению зарядов. Одним из способов ее решения является использование понятия потока вектора напряженности (потока электрического поля) и теоремы Гаусса. По определению, элементарный поток вектора напряженности dФ через элементарную площадку dS есть скалярное произведение вектора Е на вектор элемента площадки dS (рис. 1. 6). Под dS понимается вектор, направленный перпендикулярно к плоскости dS и равный по величине . Направление dS задается правилом обхода контура площадки и для замкнутых поверхностей совпадает с направлением внешней нормали. Таким образом, элементарный поток вектора Е равен

, (1. 10)

или

, (1. 11)

где a угол между векторами Е и dS. Поток вектора Е через произвольную поверхность S равен интегралу по данной поверхности:

. (1. 12)

Рассчитаем поток электрического поля точечного заряда q через сферическую поверхность (рис. 1.7), центр которой совпадает c положением заряда. С учетом уравнений (1. 6) и (1. 11) получим:

, (1. 13)

где R - радиус сферической поверхности. Согласно (1. 12), поток не зависит от размеров сферы. Из рис. 1.7 видно, что число линий напряженности, пронизывающих сферическую поверхность и ее деформированную поверхность S' одинаково, т. е. поток вектора E через замкнутую поверхность произвольной формы, охватывающую заряд q,

. (1. 14)

Пусть внутри некоторой замкнутой поверхности S находится произвольное число (N) точечных зарядов любого знака. В силу принципа суперпозиции (1. 9) результирующее поле Е данной системы зарядов равно векторной сумме полей каждого из зарядов: . Тогда поток вектора Е через поверхность S, с учетом (1. 14), равен

или

. (1. 15)

Уравнение (1. 15) выражает теорему Гаусса: поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен произведению 4pk на алгебраическую сумму зарядов, охватываемых данной поверхностью.

Если же заряды находится вне замкнутой поверхности, то линии напряженности пронизывают данную поверхность дважды (сколько войдет линий напряженности, столько и выйдет). В результате поток электрического поля через поверхность, не охватывающую заряды, равен нулю.

Теорема Гаусса, во-первых, устанавливает связь между полем (Е) и его источником (q), в некотором смысле обратную той, что дает закон Кулона. Закон Кулона позволяет определить электрическое поле по заданным зарядам. По уравнению (1. 15) можно определить величину заряда в любой области, в которой известна величина поля (Е). Во-вторых, уравнение (1. 15) является мощным аналитическим инструментом при решении основной задачи электростатики.