Закон Кулона. Электрическое поле. Напряженность

Глава 1. Электрическое поле в вакууме

Все тела в природе состоят из молекул или атомов. Атомы в свою очередь состоят из ядра и электронов, обладающих электрическим зарядом. Существует два вида электрических зарядов. Их условно называют положительными и отрицательными зарядами. Носителем отрицательного элементарного (наименьшего) заряда является, например, электрон. Электрон это элементарная частица массой m _e = 9, 1 10^{-31 кг и зарядом}

e= -1, 60 10^-19 Кл. Носителем положительного элементарного заряда является, например, протон с массой m _p= 1, 67 10^{-27 кг и зарядом q} _p = 1, 60 10^-19 Кл. Протоны входят в состав ядра атомов. Поэтому ядра атомов заряжены положительно. В каждом атоме количества положительного и отрицательного заряда одинаковы, поэтому обычно тела оказываются незаряженными.

Появление на телах электрического заряда обусловлено перераспределением электронов между телами. Например, при трении шелковой ткани о стеклянную палочку (электризация трением) электроны с палочки переходят на ткань. При этом стеклянная палочка заряжается положительно, а шелк - отрицательно. Опыты показывают, что тела могут иметь лишь заряд q равный целому кратному элементарного заряда e:

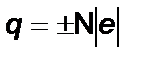(1. 1)

где N=1, 2, 3 ¼.

В замкнутой системе алгебраическая сумма зарядов тел (частиц) остается величиной постоянной:

. (1. 2)

Уравнение (1. 2) выражает закон сохранения электрического заряда. Данный закон надежно проверен в многочисленных точных физических экспериментах. Между заряженными телами (в дальнейшем будем говорить между зарядами) возникают особые силы взаимодействия, называемые электрическими силами.

Из опытов следует, что между разноименными зарядами возникают силы притяжения, между одноименными - силы отталкивания.

Рассмотрим взаимодействие точечных электрических зарядов. Точечным электрическим зарядом называется заряженное тело, размерамикоторого можно пренебречь в условиях данной задачи. Известно, что взаимодействие точечных неподвижных зарядов описывается законом Кулона: два неподвижных точечных заряда в вакууме отталкивают или притягивают друг друга с силой, пропорционально произведению величин зарядов и обратно пропорционально квадрату расстояния между ними:

. (1. 3)

Запишем (1. 3) в векторной форме:

, (1. 4)

где F12 - сила, действующая со стороны заряда q1 на одноименный заряд q2 (рис. 1.1); r12 - расстояние между зарядами; 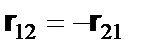- радиус-вектор, соединяющий заряды q1 и q2; -единичный вектор сонаправленный с r₁₂.

Уравнение (1. 4) отражает и тот факт, что одноименные заряды отталкиваются, а разноименные притягиваются и что сила, входящая в уравнение подчиняется третьему закону Ньютона:

F12=-F21.

Закон Кулона является основным законом электростатики - учения об электрическом взаимодействии неподвижных зарядов.

Коэффициент k в (1. 4) по особым соображениям принято выбирать в системе СИ в виде

,

где e0=8, 85 · 10-12 Кл2/(Н× м2) – электрическая постоянная, поэтому k=9, 0 ·109 Н·м2/Кл2.

Согласно современным представлениям, передача силовых взаимодействий между разобщенными телами не может осуществляться без участия материи. Всякое действие передается с помощью материального объекта, причем с конечной скоростью. И в тех случаях, когда между отдельными телами нет никакого вещества (вакуум), взаимодействие тел осуществляется посредством особого материального объекта - поля. Поле существует реально так же, как и вещество. Частицы и поле – два вида материи.

В пространстве, окружающем заряд, всегда существует поле, порожденное этим зарядом ‑ электрическое поле. Электрическое поле неподвижных зарядов называется электростатическим. Основным свойством электрического поля является его способность действовать с некоторой силой на заряды (как движущиеся, так и неподвижные), помещенные в данное поле. Важной характеристикой электрического поля является напряженность. Чтобы вычислить напряженность электрического поля E в некоторой точке, нужно разделить силу F, с которой электрическое поле действует на заряд q0, помещенный в данную точку, на его величину. При этом нужно убедиться, что присутствие заряда q0 не меняет положения зарядов, создающих данное поле. Таким образом,

. (1. 5)

Направление вектора E совпадает с направлением силы, действующей на положительный заряд.

Если электрическое поле создается неподвижным точечным зарядом q, то напряженность поля в точке А, находящейся на расстоянии r от q (рис. 1.2), с учетом уравнений (1. 4) и (1. 5) равна:

. (1. 6)

Напряженность является силовой электрического поля. Сила, действующая со стороны поля на произвольный точечный заряд q,

равна

. (1. 7)

Из опытов следует, что сила, с которой система точечных зарядов действует на некоторый точечный заряд, равна векторной сумме сил, с которыми действует на него каждый из зарядов системы. Таким образом, электрическое поле системы зарядов определяется векторной суммой напряженностей полей, создаваемых отдельными зарядами системы:

. (1. 8)

Уравнение (1. 8) выражает принцип суперпозиции электрических полей. На рис. 1.3 показано как находить напряженность поля в точке А, создаваемого системой из двух точечных зарядов.

Используя уравнения (1. 6) и (1. 8), рассчитаем поле диполя. Под диполем понимается система из двух равных по величине, но противоположных по знаку точечных электрических зарядов, расположенных на расстоянии l, малом по сравнению с расстоянием r до интересующей нас точки поля. Диполь характеризуется электрическим моментом:

,

где l - плечо диполя. Электрический момент диполя – вектор, направленный по оси диполя от его отрицательного заряда к положительному.

Определим напряженность поля в точке А, расположенной на оси диполя (рис. 1.3):

,

где напряженность поля, создаваемого зарядом +q, Е-А–зарядом -q. Так как эти вектора направлены в противоположные стороны, получим:

.

Напряженность поля диполя для точек (точка В), расположенных на перпендикуляре к оси диполя, проходящем посредине между зарядами (рис. 1.3), найдем из подобия треугольников В+q-q и ВЕ+Е: 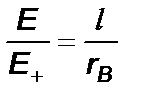или

,

где r–расстояние от оси диполя до точки В. Можно показать, что и для всех точек поля (при r > > l)

. (1. 9)

Таким образом, напряженность поля диполя убывает как третья степень расстояния.