Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Дислокационные конфигурации

Дислокации взаимодействуют друг с другом и образуют дислокационные конфигурации.

1. Рассмотрим сначала взаимодействие между двумя параллельными краевыми дислокациями (рис.3.16) с осями вдоль оси z и b ≡ b _х.

Дислокация 1 создает в точке (х ₂; у ₂) напряжения, определяемые формулами (3.15). Подставляя (3.15) в формулу (3.22) и учитывая b ≡ b _х и l ≡ l _z, получаем для силы, действующей на дислокацию 2, F = F _x в плоскости ее скольжения xz, выражение

, (3.23)

где (b·b) - скалярное произведение векторов, τ ^* − теоретическая прочность на сдвиг.

Из этой формулы видно, что F_x = 0 при x ₂ = 0 и при x ₂ =±y ₂. При х< у сила отрицательная, а при х> у положительная, т. е. точки х ₂ =±y ₂ (2’’’) являются точками неустойчивого равновесия, а точка х ₂ = 0 – устойчивого равновесия (2’).

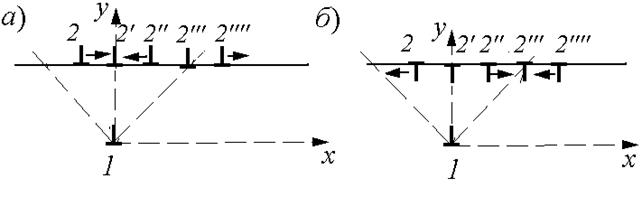
Рис. 3.16. Силы, действующие со стороны дислокации 1 на дислокацию 2 в различных положениях последней, при одинаковых (а) и противоположных (б) векторах Бюргерса.

Стрелки при дислокациях указывают направление действия силы. Отсутствие стрелки означает F =0, т.е. положение равновесия

Действительно, силы, действующие на дислокацию 2, направлены от точек x ₂ = ± y ₂ к точке х ₂ = 0 (рис. 3.16, а). При изменении знака вектора Бюргерса одной из дислокации, например дислокации 2 (рис. 3.16, б), b_х= – b меняется знак силы в формуле (3.23) и все направления сил меняются на обратные.

Таким образом, возможны два типа устойчивых конфигураций – типа стенки для одноименных дислокаций (рис. 3.17, б) и шахматная для разноименных (рис. 3.17, в).

Можно показать, что для винтовых дислокаций устойчивые конфигурации отсутствуют: разноименные дислокации всегда притягиваются; а одноименные - отталкиваются. Винтовые дислокации способны образовать устойчивую конфигурацию, только если есть два типа дислокаций, отличающихся направлением осей и, следовательно, вектором Бюргерса.

Рассмотрим подробнее скопление дислокаций и дислокационную стенку.