💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Энергия дислокации

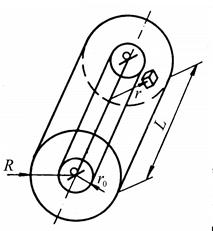
Кристалл, содержащий дислокацию, обладает собственной энергией W _д, большей, чем энергия W _иидеального кристалла из такого же числа атомов. Избыток энергии Δ W=W _д -W _и называется собственной энергией дислокации. Вычислим собственную энергию прямолинейной винтовой дислокации Δ W _в≡ W _в, проходящей по оси цилиндрического кристалла радиусом R и длиной L (рис.3.14). В элементе объема dV(r), расположенном на расстоянии r от оси дислокации, согласно формуле (3.14) создаются напряжения τ (r) = 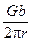. Согласно линейной теории упругости это означает, что объем

dV (r)= rd j drdz

обладает избыточной упругой энергией

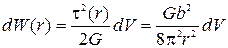. (3.16)

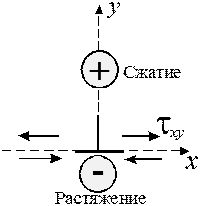
Рис. 3.13. Характер напряжений, создаваемых краевой дислокацией	Рис. 3.14. Выбор элемента объема при вычислении энергии винтовой дислокации

Полная энергия дислокации получится из (3.16), если dW (r)проинтегрировать по всему объему кристалла:

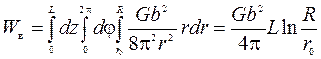. (3.17)

Формула (3.17) учитывает энергию упругих напряжений, действующих в полом цилиндре с радиусами r ₀ и R, но не учитывает энергии ядра дислокации, т.е. энергии упругих напряжений при r< r ₀. В ядре дислокации методы механики сплошной среды неприменимы, поэтому оценка энергии ядра дислокации носит приближенный характер. Для оценочных расчетов принимают

, (3.18)

где Z учитывает энергию ядра дислокации, причем Z ≈ 1÷ 3.

Оценки вклада дальнодействующих напряжений в энергию дислокации показывают, что W _в зависит от радиуса R, т.е. от размера контура, по которому выполняют интегрирование (3.17). Радиус интегрирования R часто называют «радиусом экранирования» напряжений от дислокации. В выборе R существует некоторый произвол, поскольку при R ®¥ энергия дислокации бесконечно велика, а при R ® r ₀ W _в®0. В связи с этим приближенно принимают R _min≈ 100 r ₀≈ 500·10^{− 10} м, а R _max≈ 0, 1 мкм = 10^{− 7} м, что равно среднему расстоянию между дислокациями.

Среднее значение логарифма в (3.18) составляет (подставляем среднее геометрическое R=R_ср=Ö R_minR_max)

.

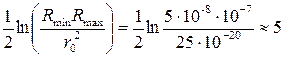С учетом энергии ядра Z= 1÷ 3 можно принять упрощенное выражение для оценки энергии ядра винтовой дислокации

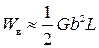. (3.19)

Энергия краевой дислокации W _к вычисляется совершенно аналогично, только из-за большего числа компонентов напряжения расчеты более громоздки. Результат вычислений имеет вид

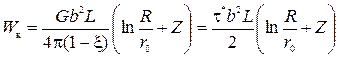, (3.20)

где 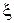- коэффициент Пуассона.

Можно написать общую формулу для энергии дислокации W _д:

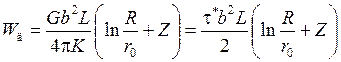, (3.21)

где K = 1 для винтовой, К = 1 – ξ для краевой и 1–ξ < K < 1 для смешанной дислокации; τ * - напряжение сдвига в идеальном кристалле (см.гл.1).

Таким образом, можно сделать следующие выводы:

1. Энергия дислокации пропорциональна ее длине.

2. По порядку величины энергии различных дислокаций совпадают.

3. Энергия дислокации даже длиной в одно межатомное расстояние (L = b) велика и соизмерима с энергией связи атомов:

.

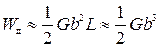При G ≈ 30 ГПа и а = 3ּ 10^–10 м 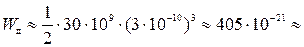2, 53 эВ.

4. Энергия дислокации пропорциональна b ² – квадрату ее вектора Бюргерса. Если проследить вывод формулы (3.21), то эта зависимость становится очевидной: W _д ~ τ ε – энергия пропорциональна произведению напряжений на деформацию, где τ ~ b и ε = τ / G.

5. Вклад в энергию дислокации от дальнодействующих напряжений, пропорциональный ln R/r ₀ = 5÷ 10, всегда больше, чем вклад от области ядра Z ≈ l÷ 3.